Përmbajtje:
- Hapi 1:
- Hapi 2:
- Hapi 3: Diagrami i Tensionit dhe Fazorit Aktual për Format e Valëve
- Hapi 4: Këndet e fazës aktuale, të rezistencës dhe të tensionit të qarqeve të serive RC
- Hapi 5: Pengesa dhe Këndi i Fazës së Qarqeve të Serisë RC
- Hapi 6: Ndryshimi i rezistencës me frekuencë
- Hapi 7: Ndryshimi i rezistencës dhe këndi i fazës me frekuencë
- Hapi 8: Një ilustrim se si Z dhe XC ndryshojnë me frekuencë
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 12:10.
- E modifikuara e fundit 2025-01-23 15:10.

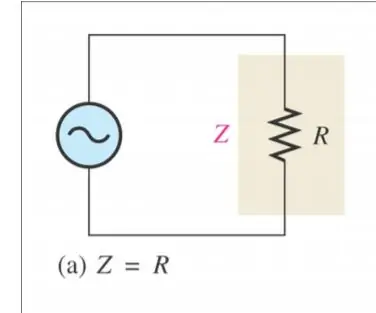
Qarqet RC
Pengesa: është ajo që burimi "Shikon" si Kundërshtim total ndaj Rrymës
Metoda e llogaritjes së rezistencës ndryshon nga një qark
Hapi 1:

Kur një qark është thjesht kapacitiv (përmban vetëm kondensatorin), këndi i fazës midis tensionit të aplikuar dhe rrymës totale është 90 ° (Rrymat aktuale)
Hapi 2:

Kur ekziston një kombinim i rezistencës dhe kapacitetit në një qark, këndi i fazës midis rezistencës (R) dhe reaktancës kapacitive (XC) është 90 ° dhe këndi i fazës për rezistencën totale (Z) është diku midis 0 ° dhe 90 °
Kur ekziston një kombinim i rezistencës dhe kapacitetit në një qark, këndi i fazës midis rrymës totale (IT) dhe tensionit të kondensatorit (VC) është 90 ° dhe këndi i fazës midis tensionit të aplikuar (VS) dhe rrymës totale (IT) është diku midis 0 ° dhe 90 °, në varësi të vlerave relative të rezistencës dhe kapacitetit
Hapi 3: Diagrami i Tensionit dhe Fazorit Aktual për Format e Valëve

Hapi 4: Këndet e fazës aktuale, të rezistencës dhe të tensionit të qarqeve të serive RC

Hapi 5: Pengesa dhe Këndi i Fazës së Qarqeve të Serisë RC

- Në qarkun serik RC, rezistenca totale është shuma fazore e R dhe Xc
- Madhësia e rezistencës: Z = √ R^2 + Xc^2 (Shuma vektoriale)
- Këndi i fazës: θ = tan-1 (X C/R)
Pse e përdorim shumën vektoriale jo shumën algjebrike?
Përgjigje: Sepse Rezistenca nuk e vonon tensionin, por Kondensatori e bën këtë.
Pra, Z = R+Xc është i gabuar.
Zbatimi i ligjit të Ohmit në një seri të tërë qarku RC përfshin përdorimin e sasive Z, Vs dhe Itot si:
Itot = Vs/Z Z = Vs/Itot Vs = Itot * Z
Gjithashtu mos harroni:
Xc = 1/2πFC
Hapi 6: Ndryshimi i rezistencës me frekuencë

Hapi 7: Ndryshimi i rezistencës dhe këndi i fazës me frekuencë

Hapi 8: Një ilustrim se si Z dhe XC ndryshojnë me frekuencë

R mbetet konstante
Recommended:
Helmeta e Sigurisë Covid Pjesa 1: Një Hyrje në Qarqet Tinkercad !: 20 hapa (me fotografi)

Helmeta e Sigurisë Covid Pjesa 1: Një Hyrje në Qarqet Tinkercad !: Përshëndetje, mik! Në këtë seri me dy pjesë, ne do të mësojmë se si të përdorim Qarqet e Tinkercad - një mjet argëtues, i fuqishëm dhe edukativ për të mësuar se si funksionojnë qarqet! Një nga mënyrat më të mira për të mësuar, është të bësh. Pra, ne së pari do të hartojmë projektin tonë personal: th
Hyrje në qarqet IR: 8 hapa (me fotografi)

Hyrje në Qarqet IR: IR është një pjesë komplekse e teknologjisë por shumë e thjeshtë për të punuar me të. Ndryshe nga LED ose LASER, Infrared nuk mund të shihet me syrin e njeriut. Në këtë Udhëzues, unë do të demonstrojë përdorimin e Infrared përmes 3 qarqeve të ndryshme. Qarqet nuk do të jenë u
Qarqet Snap Robot Telepresence: 9 hapa

Roboti Telepresence i Qarqeve Snap: Pushimet në vitin 2020 janë pak më ndryshe. Familja ime është e përhapur në të gjithë vendin, dhe për shkak të pandemisë ne nuk jemi në gjendje të mblidhemi së bashku për pushime. Doja një mënyrë për t'i bërë gjyshërit të ndiheshin të përfshirë në festën tonë të Falënderimeve. Një telepresë
Radio FM Nga Qarqet Snap: 13 Hapa

Radio FM Nga Qarqet Snap: duke përdorur sistemin Elenco Snap Circuits
Qarqet MakeyMakey: 3 hapa
Qarqet MakeyMakey: Ne përziejmë në tabelë një dërrasë të prodhimit, disa tela krokodili dhe disa objekte elektrike përçuese. Me disa projekte ndërvepruese në zero ne ndërtojmë qarqe për të bashkëvepruar me kompjuterin ose/dhe me objektet
