EWEEDINATOR☠ Pjesa 4: Gjeometria diferenciale e drejtimit Kodi: 3 hapa

2025 Autor: John Day | [email protected]. E modifikuara e fundit: 2025-01-23 15:10

Nëse keni kohë për të parë videon e mësipërme, do të vini re se ka disa zhurma të çuditshme të shkaktuara nga motorët në ngecjen e timonit herë pas here ndërsa WEEDINATOR lundron në një kthesë me 3 pikë. Motorët në thelb bllokohen kundër njëri -tjetrit pasi rrezja e kthesës është e ndryshme nga brenda në pjesën e jashtme dhe distanca që rrota udhëton është e ndryshme për shkallën e kthesës.

Gjeometria e kthesës mund të përpunohet duke skicuar 8 ose më shumë ndërrime të kthesës, duke dhënë shembuj të rrotullimit në kënde të ndryshme në rrotën e brendshme nga 0 (pa kthesë) në 90 (bllokim i plotë) gradë. Tingëllon e komplikuar?

Shumica e robotëve me rrota të vogla nuk përpiqen të kenë ndonjë lloj drejtimi të sofistikuar dhe mbështeten, në mënyrë shumë efektive, në thjesht ndryshimin e shpejtësisë relative të motorëve në secilën anë të automjetit, e cila është pothuajse e njëjtë me atë se si një gërmues ose tank punon. Kjo është e mrekullueshme nëse jeni duke ngarkuar mbi një zonë lufte të mbushur me krater duke qëlluar gjithçka që lëviz, por në një mjedis të qetë bujqësor është e rëndësishme të bëni sa më pak dëme në tokë dhe tokë, kështu që rrotat e bluarjes përpara dhe përpara kundër njëri -tjetrit është Jo e pershtatshme!

Shumica e makinave dhe traktorëve kanë një vegël shumë të dobishme të quajtur "Diferencial", përveç makinave që shihni në filmat e vjetër amerikanë ku mund të dëgjoni gomat që kërcisin si të çmendura sa herë që shkojnë në një qoshe. A ndërtojnë ende amerikanët makina si kjo? Me WEEDINATOR, ne mund të programojmë diferencial në motorët e vozitjes duke përpunuar formulën për shpejtësitë dhe këndet relative të rrotave në çdo kënd të veçantë të kthesës. Akoma tingëllon e komplikuar?

Këtu është një shembull i shpejtë:

Nëse WEEDINATOR po lundron në një kthesë dhe e ka timonin brenda në 45 gradë, rrota e jashtme NUK është 45 gradë, është më shumë si 30 gradë. Gjithashtu, rrota e brendshme mund të kthehet me 1 km/orë, por rrota e jashtme do të jetë dukshëm më e shpejtë, më shumë se 1.35 km/orë.

Hapi 1: Konfigurimi i gjeometrisë

Disa supozime themelore bëhen për të filluar me:

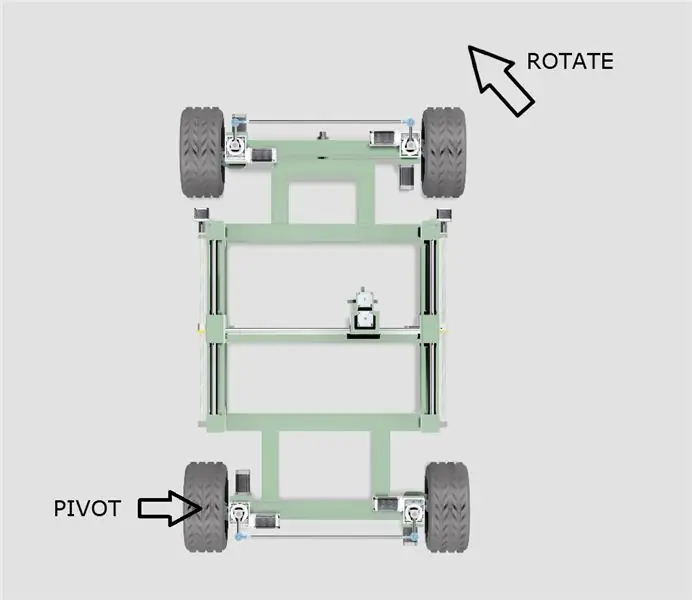
• Shasia do të rrotullohet rreth njërës prej rrotave të pasme siç tregohet në diagramin e mësipërm.
• Qendra efektive e rrethit rrotullues do të lëvizë përgjatë një linje të shtrirë nga qendrat e dy rrotave të pasme, në varësi të këndit të kthesës.
• Gjeometria do të marrë formën e një kurbë sinus.

Hapi 2: Vizatimet e shkallëzuara të këndeve të rrotave dhe rrezeve

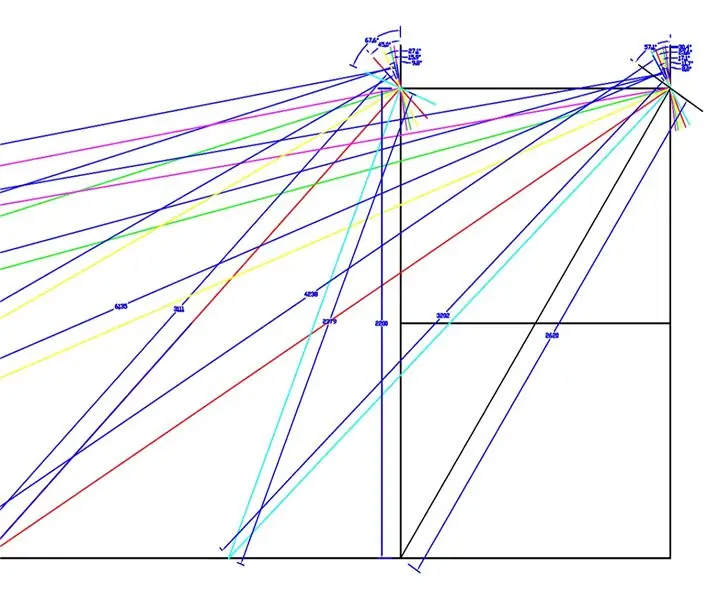
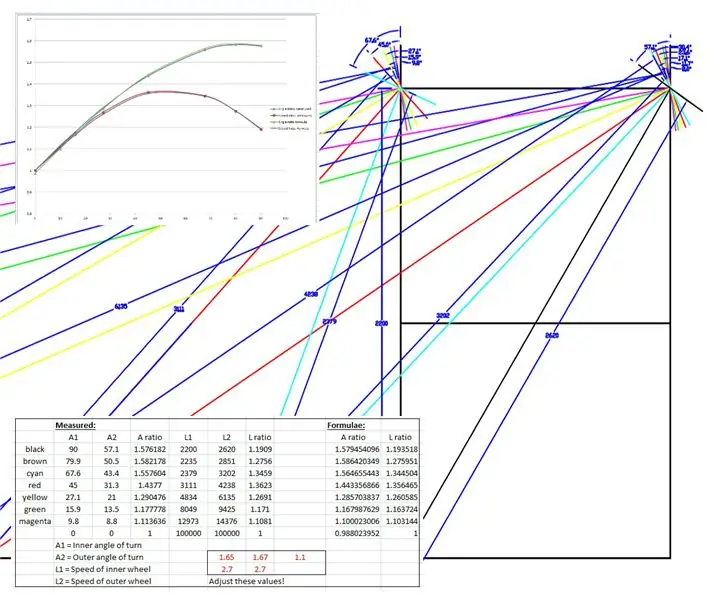
Një vizatim në shkallë të plotë u bë nga rrotat dhe shasia e përparme WEEDINATOR me 8 ndryshime të ndryshme të këndit të rrotave brenda 0 dhe 90 gradë dhe qendrat përkatëse të kthesës u hartuan siç tregohet në vizatimet e mësipërme.

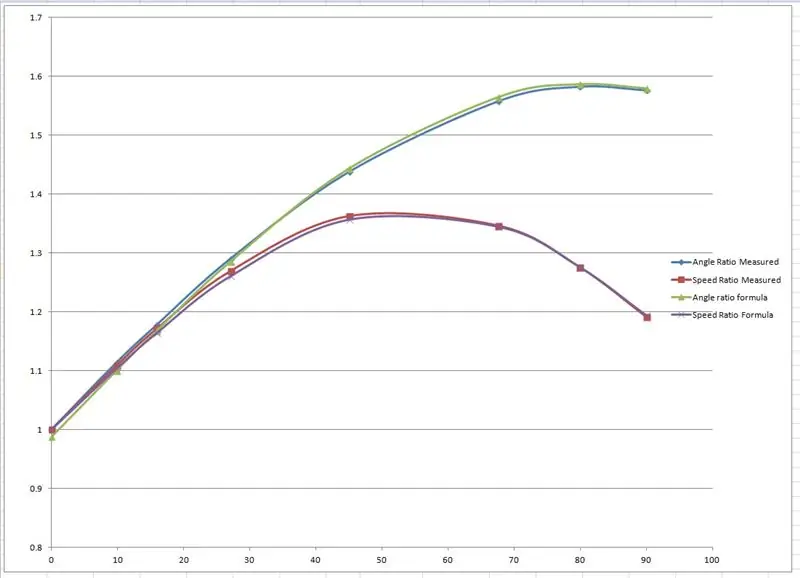
Rrezet efektive u matën nga vizatimi dhe u vizatuan në një grafik në Microsoft Excel.

U prodhuan dy grafikë, një i raportit të boshteve të rrotave të përparme të majtë dhe të djathtë dhe një tjetër për raportin e dy rrezeve për secilin kënd të veçantë të kthesës.

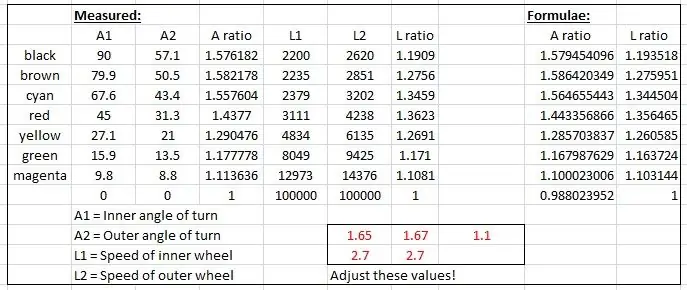
Unë pastaj 'fudged' disa formula për të imituar rezultatet empirike bazuar në një kurbë sinus. Një nga fudgings duket kështu:

speedRatio = (mëk (e brendshme*1.65*pi/180) +2.7) /2.7; // e brendshme është këndi i brendshëm i kthesës.

Kthesat u falsifikuan duke ndryshuar vlerat e treguara me të kuqe në skedarin excel derisa kthesat të vendosen së bashku.

Hapi 3: Kodimi i formulave

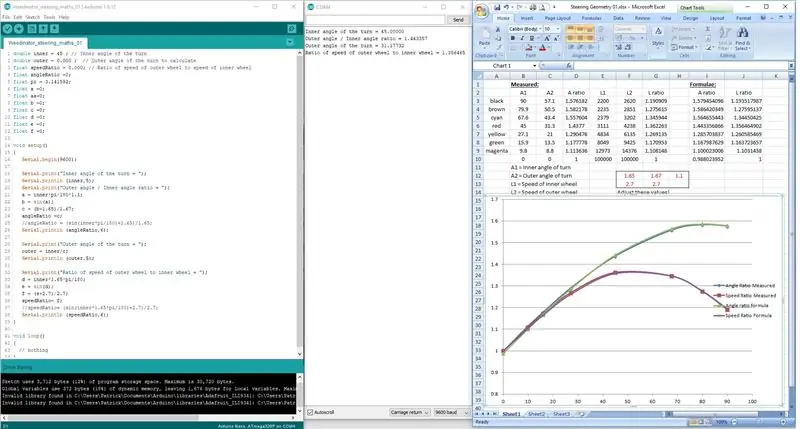
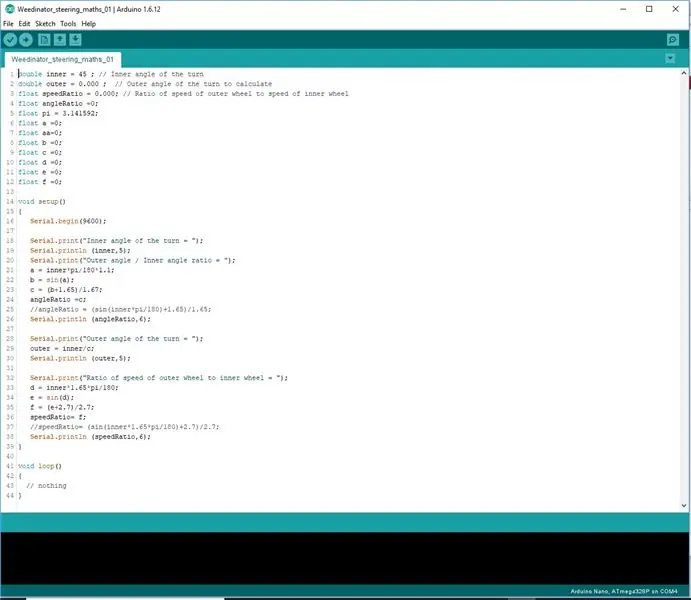
Në vend që të përpiqen të kodojnë formulat në një rresht, ato u ndanë në 3 faza për të lejuar që Arduino të përpunojë matematikën siç duhet.

Rezultatet tregohen në ekranin e portit serik dhe kontrollohen me rezultatet e matura në vizatimin e shkallës.