
Përmbajtje:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 12:35.
- E modifikuara e fundit 2025-01-23 15:10.
Prezantimi
Ky udhëzues u drejtohet të gjithëve të interesuar në përdorimin e Përshpejtuesve dhe Xhiroskopëve, si dhe pajisjeve të kombinuara IMU (Njësia e Matjes Inerciale) në projektet e tyre elektronike
Ne do të mbulojmë:
- Çfarë mat një akselerometër?
- Çfarë mat një xhiroskop (i njohur si xhiro)?
- Si të konvertoni leximet analoge në dixhitale (ADC) që merrni nga këta sensor në njësi fizike (ato do të ishin g për përshpejtues, deg/s për xhiroskop)
- Si të kombinoni leximet e përshpejtuesit dhe xhiroskopit në mënyrë që të merrni informacion të saktë në lidhje me prirjen e pajisjes tuaj në lidhje me rrafshin tokësor
Gjatë gjithë artikullit do të përpiqem ta mbaj matematikën në minimum. Nëse e dini se çfarë janë Sine/Cosine/Tangent atëherë ju duhet të jeni në gjendje të kuptoni dhe përdorni këto ide në projektin tuaj pavarësisht se çfarë platforme po përdorni: Arduino, Propeller, Basic Stamp, patate të skuqura Atmel, Microchip PIC, etj.
Ka njerëz atje që besojnë se keni nevojë për matematikë komplekse në mënyrë që të përdorni një njësi IMU (filtra komplekse FIR ose IIR siç janë filtrat Kalman, filtrat Parks-McClellan, etj). Ju mund t'i hulumtoni të gjitha ato dhe të arrini rezultate të mrekullueshme por komplekse. Mënyra ime për të shpjeguar gjërat kërkon vetëm matematikë bazë. Unë jam një besimtar i madh në thjeshtësinë. Unë mendoj se një sistem që është i thjeshtë është më i lehtë për tu kontrolluar dhe monitoruar, përveç që shumë pajisje të ngulitura nuk kanë fuqinë dhe burimet për të zbatuar algoritme komplekse që kërkojnë llogaritjet e matricës.
Unë do të përdor si shembull një njësi të re të IMU -së, Acc_Gyro Accelerometer + Gyro IMU. Ne do të përdorim parametrat e kësaj pajisjeje në shembujt tanë më poshtë. Kjo njësi është një pajisje e mirë për të filluar, sepse përbëhet nga 2 pajisje:
- LIS331AL (fletë të dhënash) - një përshpejtues triaksial 2G - LPR550AL (fletë të dhënash) - një hap dhe rrotullim me bosht të dyfishtë, xhiroskop 500 deg/sek
Së bashku ata përfaqësojnë një Njësi të Matjes Inerciale të 5 Shkallëve të Lirisë. Tani ky është një emër i zbukuruar! Sidoqoftë, prapa emrit të zbukuruar është një pajisje kombinimi shumë e dobishme që ne do të mbulojmë dhe shpjegojmë në detaje në këtë udhëzues.
Hapi 1: Përshpejtuesi
Për të kuptuar këtë njësi do të fillojmë me përshpejtuesin. Kur mendoni për përshpejtuesit është shpesh e dobishme të imazhoni një kuti në formën e një kubi me një top brenda tij. Ju mund të imagjinoni diçka tjetër si një cookie ose një donut, por unë do të imagjinoj një top:
Nëse e marrim këtë kuti në një vend pa fusha gravitacioni ose për atë çështje pa fusha të tjera që mund të ndikojnë në pozicionin e topit - topi thjesht do të notojë në mes të kutisë. Mund ta imagjinoni se kutia është në hapësirën e jashtme shumë larg nga çdo trup kozmik, ose nëse një vend i tillë është i vështirë për tu gjetur imagjinoni të paktën një anije kozmike që orbiton rreth planetit, ku gjithçka është në gjendje pa peshë. Nga fotografia e mësipërme mund të shihni që secilit aks i caktojmë një palë mure (hoqëm murin Y+ në mënyrë që të shikojmë brenda kutisë). Imagjinoni që çdo mur është i ndjeshëm ndaj presionit. Nëse lëvizim papritur kutinë në të majtë (e përshpejtojmë me nxitim 1g = 9.8m/s^2), topi do të godasë murin X-. Ne pastaj matim forcën e presionit që topi aplikon në mur dhe nxjerrim një vlerë prej -1g në boshtin X.
Ju lutemi vini re se akselerometri në të vërtetë do të zbulojë një forcë që drejtohet në drejtim të kundërt nga vektori i nxitimit. Kjo forcë shpesh quhet Forca Inerciale ose Forca Fiktive. Një gjë që duhet të mësoni nga kjo është se një akselerometër mat nxitimin në mënyrë indirekte përmes një force që aplikohet në njërin prej mureve të tij (sipas modelit tonë, mund të jetë një burim ose diçka tjetër në përshpejtuesit e jetës reale). Kjo forcë mund të shkaktohet nga nxitimi, por siç do të shohim në shembullin tjetër ajo nuk shkaktohet gjithmonë nga nxitimi.
Nëse marrim modelin tonë dhe e vendosim në Tokë, topi do të bjerë në murin Z dhe do të aplikojë një forcë prej 1g në murin e poshtëm, siç tregohet në foton më poshtë:
Në këtë rast, kutia nuk lëviz, por ne ende marrim një lexim prej -1g në boshtin Z. Presioni që topi ka ushtruar në mur u shkaktua nga një forcë gravitacionale. Në teori mund të jetë një forcë e ndryshme - për shembull, nëse imagjinoni që topi ynë është metalik, vendosja e një magneti pranë kutisë mund ta lëvizë topin në mënyrë që të godasë një mur tjetër. Kjo u tha vetëm për të vërtetuar se në thelb masat e përshpejtuesit matin forcën dhe jo nxitimin. Thjesht ndodh që nxitimi të shkaktojë një forcë inerciale që kapet nga mekanizmi i zbulimit të forcës së përshpejtuesit.
Ndërsa ky model nuk është saktësisht se si është ndërtuar një sensor MEMS, ai është shpesh i dobishëm në zgjidhjen e problemeve të lidhura me akselerometrin. Në të vërtetë ka sensorë të ngjashëm që kanë topa metalikë brenda, ata quhen çelësa pjerrësie, megjithatë ata janë më primitivë dhe zakonisht ata mund të tregojnë vetëm nëse pajisja është e prirur brenda një diapazoni apo jo, jo shkallën e prirjes.
Deri më tani ne kemi analizuar daljen e akcelerometrit në një aks të vetëm dhe kjo është gjithçka që do të merrni me një akselerometër me një aks të vetëm. Vlera reale e akselerometrave triaksial vjen nga fakti se ato mund të zbulojnë forcat inerciale në të tre akset. Le të kthehemi në modelin tonë të kutisë dhe ta rrotullojmë kutinë 45 gradë në të djathtë. Topi do të prekë tani 2 mure: Z- dhe X- siç tregohet në foton më poshtë:
Vlerat e 0.71 nuk janë arbitrare, ato janë në të vërtetë një përafrim për SQRT (1/2). Kjo do të bëhet më e qartë ndërsa prezantojmë modelin tonë të ardhshëm për përshpejtuesin.
Në modelin e mëparshëm ne kemi fiksuar forcën e gravitetit dhe kemi rrotulluar kutinë tonë imagjinare. Në 2 shembujt e fundit ne kemi analizuar daljen në 2 pozicione të ndryshme të kutisë, ndërsa vektori i forcës mbeti konstant. Ndërsa kjo ishte e dobishme për të kuptuar se si akselerometri ndërvepron me forcat e jashtme, është më praktike të kryhen llogaritjet nëse e rregullojmë sistemin koordinativ në akset e përshpejtuesit dhe imagjinojmë se vektori i forcës rrotullohet rreth nesh.
Ju lutemi hidhini një sy modelit të mësipërm, unë kam ruajtur ngjyrat e akseve në mënyrë që të bëni një kalim mendor nga modeli i mëparshëm në atë të ri. Vetëm imagjinoni që çdo bosht në modelin e ri është pingul me faqet përkatëse të kutisë në modelin e mëparshëm. Vektori R është vektori i forcës që mat akselerometri (mund të jetë ose forca e gravitacionit ose forca inerciale nga shembujt e mësipërm ose një kombinim i të dyjave). Rx, Ry, Rz janë projeksion i vektorit R në boshtet X, Y, Z. Ju lutemi vini re lidhjen e mëposhtme:
R^2 = Rx^2 + Ry^2 + Rz^2 (barazimi 1)
i cili në thelb është ekuivalent i teoremës së Pitagorës në 3D.
Mos harroni se pak më herët ju thashë se vlerat e SQRT (1/2) ~ 0.71 nuk janë të rastësishme. Nëse i lidhni ato në formulën e mësipërme, pasi kujtoni se forca jonë e gravitetit ishte 1 g, ne mund të verifikojmë se:
1^2 = (-SQRT (1/2))^2 + 0^2 + (-SQRT (1/2))^2
thjesht duke zëvendësuar R = 1, Rx = -SQRT (1/2), Ry = 0, Rz = -SQRT (1/2) në Eq.1
Pas një hyrje të gjatë të teorisë, ne po i afrohemi akselerometrave të jetës reale. Vlerat Rx, Ry, Rz janë në të vërtetë të lidhura në mënyrë lineare me vlerat që do të nxjerrë përshpejtuesi juaj i jetës reale dhe që mund t'i përdorni për kryerjen e llogaritjeve të ndryshme.
Para se të arrijmë atje, le të flasim pak për mënyrën se si akselerometrat do të na japin këtë informacion. Shumica e akcelerometrave ndahen në dy kategori: dixhitale dhe analoge. Përshpejtuesit dixhital do t'ju japin informacion duke përdorur një protokoll serik si I2C, SPI ose USART, ndërsa përshpejtuesit analogë do të japin një nivel tensioni brenda një diapazoni të paracaktuar që duhet të konvertoni në një vlerë dixhitale duke përdorur një modul ADC (konvertues analog në dixhital). Unë nuk do të hyj në shumë detaje se si funksionon ADC, pjesërisht sepse është një temë kaq e gjerë dhe pjesërisht sepse është e ndryshme nga njëra platformë në tjetrën. Disa mikrokontrollues do të kenë module të integruara ADC, disa prej tyre do të kenë nevojë për përbërës të jashtëm për të kryer konvertimet ADC. Pavarësisht se çfarë lloji të modulit ADC përdorni, do të përfundoni me një vlerë në një gamë të caktuar. Për shembull, një modul ADC 10 -bit do të nxjerrë një vlerë në intervalin 0..1023, vini re se 1023 = 2^10 -1. Një modul ADC 12-bitësh do të nxjerrë një vlerë në intervalin 0..4095, vini re se 4095 = 2^12-1.
Le të vazhdojmë duke marrë parasysh një shembull të thjeshtë, supozoni se moduli ynë 10bit ADC na dha vlerat e mëposhtme për tre kanalet e akselerometrit (akset):
AdcRx = 586 AdcRy = 630 AdcRz = 561
Çdo modul ADC do të ketë një tension reference, le të supozojmë në shembullin tonë se është 3.3V. Për të kthyer një vlerë adc 10bit në tension ne përdorim formulën e mëposhtme:
VoltsRx = AdcRx * Vref / 1023
Një shënim i shpejtë këtu: se për AD -në 8bit ndarësi i fundit do të ishte 255 = 2 ^ 8 -1, dhe për 12bit ADC pjestuesi i fundit do të ishte 4095 = 2 ^ 12 -1.
Duke aplikuar këtë formulë në të 3 kanalet marrim:
VoltRx = 586 * 3.3V / 1023 = ~ 1.89V (i rrumbullakosim të gjitha rezultatet në 2 pikë dhjetore) VoltRy = 630 * 3.3V / 1023 = ~ 2.03V VoltRz = 561 * 3.3V / 1023 = 8 1.81V
Çdo akselerometër ka një nivel tensioni zero-g, mund ta gjeni në specifikimet, ky është tensioni që korrespondon me 0g. Për të marrë një vlerë të nënshkruar të tensionit, duhet të llogarisim zhvendosjen nga ky nivel. Le të themi se niveli ynë i tensionit 0g është VzeroG = 1.65V. Ne llogarisim zhvendosjet e tensionit nga tensioni zero-g si më poshtë::
DeltaVoltsRx = 1.89V - 1.65V = 0.24V DeltaVoltsRy = 2.03V - 1.65V = 0.38V DeltaVoltsRz = 1.81V - 1.65V = 0.16V
Ne tani kemi leximet tona të përshpejtuesit në Volt, ende nuk është në g (9.8 m/s^2), për të bërë konvertimin përfundimtar ne aplikojmë ndjeshmërinë e përshpejtuesit, zakonisht të shprehur në mV/g. Le të themi Ndjeshmëria jonë = 478.5mV/g = 0.4785V/g. Vlerat e ndjeshmërisë mund të gjenden në specifikimet e përshpejtuesit. Për të marrë vlerat përfundimtare të forcës të shprehura në g ne përdorim formulën e mëposhtme:
Rx = DeltaVoltsRx / Ndjeshmëria
Rx = 0.24V / 0.4785V / g = ~ 0.5g Ry = 0.38V / 0.4785V / g = ~ 0.79g Rz = 0.16V / 0.4785V / g = ~ 0.33g
Ne sigurisht që mund të kombinojmë të gjithë hapat në një formulë, por unë i kalova të gjitha hapat për ta bërë të qartë sesi kaloni nga leximet ADC në një komponent vektor të forcës të shprehur në g.
Rx = (AdcRx * Vref / 1023 - VzeroG) / Ndjeshmëria (Eku.2) Ry = (AdcRy * Vref / 1023 - VzeroG) / Ndjeshmëria Rz = (AdcRz * Vref / 1023 - VzeroG) / Ndjeshmëria
Tani kemi të tre përbërësit që përcaktojnë vektorin tonë të forcës inerciale, nëse pajisja nuk i nënshtrohet forcave të tjera përveç gravitacionit, mund të supozojmë se ky është drejtimi i vektorit të forcës sonë të gravitetit. Nëse doni të llogaritni pjerrësinë e pajisjes në lidhje me tokën, mund të llogaritni këndin midis këtij vektori dhe boshtit Z. Nëse jeni të interesuar edhe për drejtimin e pjerrësisë sipas boshtit, mund ta ndani këtë rezultat në 2 përbërës: prirja në boshtin X dhe Y që mund të llogaritet si këndi midis vektorit të gravitetit dhe boshteve X / Y. Llogaritja e këtyre këndeve është më e thjeshtë nga sa mund të mendoni, tani që kemi llogaritur vlerat për Rx, Ry dhe Rz. Le të kthehemi në modelin tonë të fundit të përshpejtuesit dhe të bëjmë disa shënime shtesë:
Këndet që na interesojnë janë këndet midis boshteve X, Y, Z dhe vektorit të forcës R. Ne do t'i përcaktojmë këto kënde si Axr, Ayr, Azr. Ju mund të vini re nga trekëndëshi me kënd të drejtë të formuar nga R dhe Rx se:
cos (Axr) = Rx / R, dhe në mënyrë të ngjashme: cos (Ayr) = Ry / R cos (Azr) = Rz / R
Ne mund të zbresim nga barazimi 1 që R = SQRT (Rx^2 + Ry^2 + Rz^2).
Tani mund t'i gjejmë këndet tona duke përdorur funksionin arccos () (funksioni i kundërt cos ()):
Axr = arccos (Rx/R) Ayr = arccos (Ry/R) Azr = arccos (Rz/R)
Ne kemi bërë një rrugë të gjatë për të shpjeguar modelin e përshpejtuesit, vetëm për të ardhur deri te këto formula. Në varësi të aplikacioneve tuaja, ju mund të dëshironi të përdorni ndonjë formulë të ndërmjetme që kemi nxjerrë. Ne gjithashtu do të prezantojmë modelin e xhiroskopit së shpejti dhe do të shohim se si të dhënat e përshpejtuesit dhe xhiroskopit mund të kombinohen për të siguruar vlerësime edhe më të sakta të prirjes.
Por, para se ta bëjmë këtë, le të bëjmë disa shënime më të dobishme:
cosX = cos (Axr) = Rx / R komod = cos (Ayr) = Ry / R cosZ = cos (Azr) = Rz / R
Kjo treshe shpesh quhet drejtimi kosinus, dhe në thelb përfaqëson vektorin njësi (vektor me gjatësi 1) që ka të njëjtin drejtim si vektori ynë R. Ju lehtë mund ta verifikoni që:
SQRT (cosX^2 + komod^2 + cosZ^2) = 1
Kjo është një pronë e mirë pasi na përjashton nga monitorimi i modulit (gjatësisë) së vektorit R. Shpesh, nëse jemi të interesuar vetëm për drejtimin e vektorit tonë inercial, ka kuptim të normalizojmë modulin e tij në mënyrë që të thjeshtojmë llogaritjet e tjera.
Hapi 2: Xhiroskop
Ne nuk do të prezantojmë asnjë model të barabartë kutie për xhiroskopin siç bëmë për përshpejtuesin, përkundrazi do të hidhemi drejt modelit të dytë të akcelerometrit dhe do të tregojmë se çfarë mat xhiroskopi sipas këtij modeli.
Çdo kanal xhiroskopi mat rrotullimin rreth njërit prej akseve. Për shembull, një xhiroskop me 2 akse do të masë rrotullimin rreth (ose disa mund të thonë "për") boshtet X dhe Y. Për ta shprehur këtë rrotullim në numra le të bëjmë disa shënime. Së pari le të përcaktojmë:
Rxz - është projeksioni i vektorit të forcës inerciale R në planin XZ Ryz - është projeksioni i vektorit të forcës inerciale R në planin YZ
Nga trekëndëshi i këndit të drejtë të formuar nga Rxz dhe Rz, duke përdorur teoremën e Pitagorës marrim:
Rxz^2 = Rx^2 + Rz^2, dhe në mënyrë të ngjashme: Ryz^2 = Ry^2 + Rz^2
gjithashtu vini re se:
R^2 = Rxz^2 + Ry^2, kjo mund të rrjedh nga barazimet 1 dhe më lart, ose mund të rrjedhë nga trekëndëshi me kënd të drejtë i formuar nga R dhe Ryz R^2 = Ryz^2 + Rx^2
Ne nuk do t'i përdorim këto formula në këtë artikull, por është e dobishme të shënojmë lidhjen midis të gjitha vlerave në modelin tonë.
Në vend të kësaj ne do të përcaktojmë këndin midis boshtit Z dhe Rxz, vektorëve Ryz si më poshtë:
Axz - është këndi midis Rxz (projeksioni i R në planin XZ) dhe boshtit Z Ayz - është këndi midis Ryz (projeksioni i R në planin YZ) dhe boshtit Z
Tani po i afrohemi asaj që mat xhiroskopi. Xhiroskopi mat shkallën e ndryshimeve të këndeve të përcaktuara më sipër. Me fjalë të tjera do të nxjerrë një vlerë që lidhet në mënyrë lineare me shkallën e ndryshimit të këtyre këndeve. Për ta shpjeguar këtë, le të supozojmë se ne kemi matur këndin e rrotullimit rreth boshtit Y (që do të ishte këndi Axz) në kohën t0, dhe ne e përcaktojmë atë si Axz0, më pas e kemi matur këtë kënd në një kohë të mëvonshme t1 dhe ishte Axz1. Shkalla e ndryshimit do të llogaritet si më poshtë:
RateAxz = (Axz1 - Axz0) / (t1 - t0).
Nëse e shprehim Axz në gradë, dhe kohën në sekonda, atëherë kjo vlerë do të shprehet në deg/s. Kjo është ajo që mat një xhiroskop.
Në praktikë një xhiroskop (nëse nuk është një xhiroskop dixhital i veçantë) rrallë do t'ju japë një vlerë të shprehur në deg/s. Njësoj si për përshpejtuesin do të merrni një vlerë ADC që do t'ju duhet të konvertoni në deg/s duke përdorur një formulë të ngjashme me barazimin. 2 që kemi përcaktuar për përshpejtuesin. Le të prezantojmë ADC në formulën e konvertimit të deg/s për xhiroskopin (supozojmë se po përdorim një modul ADC 10bit, për 8bit ADC zëvendësojmë 1023 me 255, për 12bit ADC zëvendësojmë 1023 me 4095).
RateAxz = (AdcGyroXZ * Vref / 1023 - VzeroRate) / Sensitivity Eq.3 RateAyz = (AdcGyroYZ * Vref / 1023 - VzeroRate) / Ndjeshmëria
AdcGyroXZ, AdcGyroYZ - merren nga moduli ynë adc dhe ato përfaqësojnë kanalet që matin rrotullimin e projeksionit të vektorit R në XZ përkatësisht në rrafshet YZ, që është ekuivalent me të thënë që rrotullimi është bërë rreth boshteve Y dhe X respektivisht.
Vref - është tensioni i referencës ADC që do të përdorim 3.3V në shembullin më poshtë VzeroRate - është tensioni me normë zero, me fjalë të tjera tensioni që nxjerr xhiroskopi kur nuk i nënshtrohet asnjë rrotullimi, për bordin Acc_Gyro është për shembull 1.23V (ju mund t'i gjeni këto vlera në specifikimet) Ndjeshmëria - është ndjeshmëria e xhiroskopit tuaj ajo shprehet në mV / (deg / s) shpesh e shkruar si mV / deg / s, në thelb ju tregon se sa mV do prodhimi i xhiroskopit rritet, nëse e rrisni shpejtësinë e rrotullimit me një deg/s. Ndjeshmëria e bordit Acc_Gyro është për shembull 2mV/deg/s ose 0.002V/deg/s
Le të marrim një shembull, supozoni se moduli ynë ADC ktheu vlerat e mëposhtme:
AdcGyroXZ = 571 AdcGyroXZ = 323
Duke përdorur formulën e mësipërme, dhe duke përdorur parametrat e specifikave të bordit Acc_Gyro do të marrim:
RateAxz = (571 * 3.3V/1023 - 1.23V)/(0.002V/deg/s) = ~ 306 deg/s RateAyz = (323 * 3.3V/1023 - 1.23V)/(0.002V/deg/s) = ~ -94 gradë/s
Me fjalë të tjera, pajisja rrotullohet rreth boshtit Y (ose mund të themi se rrotullohet në planin XZ) me një shpejtësi prej 306 deg/s dhe rreth boshtit X (ose mund të themi se rrotullohet në planin YZ) me një shpejtësi prej - 94 gradë/s Ju lutemi vini re se shenja negative do të thotë që pajisja rrotullohet në drejtim të kundërt nga drejtimi konvencional pozitiv. Sipas konventës, një drejtim i rrotullimit është pozitiv. Një fletë e mirë e specifikimit të xhiroskopit do t’ju tregojë se cili drejtim është pozitiv, përndryshe do t’ju duhet ta gjeni duke eksperimentuar me pajisjen dhe duke vënë në dukje se cili drejtim i rrotullimit rezulton në rritjen e tensionit në kunjin dalës. Kjo bëhet më së miri duke përdorur një oshiloskop pasi që sapo të ndaloni rrotullimin tensioni do të bjerë përsëri në nivelin e normës zero. Nëse jeni duke përdorur një multimetër ju duhet të mbani një normë konstante të rrotullimit për të paktën disa sekonda dhe të vini re tensionin gjatë këtij rrotullimi, pastaj krahasojeni atë me tensionin e shkallës zero. Nëse është më i madh se tensioni i shkallës zero, do të thotë që drejtimi i rrotullimit është pozitiv.
Hapi 3: Kombinimi i Accelerometer dhe Gyro
Duke i bashkuar të gjitha - Kombinimi i të dhënave të përshpejtuesit dhe xhiroskopit
Nëse jeni duke e lexuar këtë artikull, me siguri keni blerë ose po planifikoni të blini një pajisje IMU, ose ndoshta keni ndërmend të ndërtoni një nga pajisje të veçanta të përshpejtuesit dhe xhiroskopit.
Hapi i parë në përdorimin e një pajisjeje të kombinuar IMU që kombinon një përshpejtues dhe një xhiroskop është të përafrojë sistemet e tyre koordinative. Mënyra më e lehtë për ta bërë këtë është të zgjidhni sistemin koordinativ të përshpejtuesit si sistemi juaj koordinativ i referencës. Shumica e fletëve të të dhënave të përshpejtuesit do të shfaqin drejtimin e akseve X, Y, Z në lidhje me imazhin e çipit ose pajisjes fizike. Për shembull këtu janë drejtimet e akseve X, Y, Z siç tregohet në specifikimet për tabelën Acc_Gyro:
Hapat e mëtejshëm janë:
Identifikoni daljet e xhiroskopit që korrespondojnë me vlerat RateAxz, RateAyz të diskutuara më sipër. Përcaktoni nëse këto dalje duhet të përmbysen për shkak të pozicionit fizik të xhiroskopit në lidhje me përshpejtuesin
Mos supozoni se nëse një xhiroskop ka një dalje të shënuar X ose Y, ai do të korrespondojë me çdo bosht në sistemin koordinativ të përshpejtuesit, edhe nëse ky dalje është pjesë e një njësie IMU. Mënyra më e mirë është ta provoni. Duke supozuar se keni fiksuar pozicionin e xhiroskopit në lidhje me përshpejtuesin. Supozohet se kufijtë e xhiros dhe akselerometrit janë paralel me njëri -tjetrin, domethënë ju e vendosni xhiro në një kënd të shumëfishtë prej 90 gradë në raport me çipin e përshpejtuesit. Nëse keni blerë një bord të IMU shanset janë që ata të jenë tashmë të përafruar në këtë mënyrë. Ne nuk do të diskutojmë në këtë artikull modele ku xhiroskopi vendoset në një kënd të parregullt në lidhje me përshpejtuesin (le të themi 45 ose 30 gradë), edhe pse kjo mund të jetë e dobishme në disa aplikime.
Këtu është një sekuencë mostre për të përcaktuar se cila dalje e xhiroskopit korrespondon me vlerën RateAxz të diskutuar më sipër.
- filloni nga vendosja e pajisjes në pozicion horizontal. Të dy daljet X dhe Y të përshpejtuesit do të prodhojnë tension zero-g (për shembull për bordin Acc_Gyro kjo është 1.65V)
- fillimi tjetër i rrotullimit të pajisjes rreth boshtit Y, një mënyrë tjetër për të thënë është se ju e rrotulloni pajisjen në planin XZ, në mënyrë që daljet e përshpejtuesit X dhe Z të ndryshojnë dhe dalja Y të mbetet konstante. - gjatë rrotullimit të pajisjes me një shpejtësi konstante, e cila ndryshon daljen e xhiroskopit, daljet e tjera të xhiroskopit duhet të mbeten konstante - prodhimi i xhiroskopit që ndryshoi gjatë rrotullimit rreth boshtit Y (rrotullimi në rrafshin XZ) do të sigurojë vlerën hyrëse për AdcGyroXZ, nga e cila ne llogarisim RateAxz - hapi përfundimtar është të siguroni që drejtimi i rrotullimit të korrespondojë me modelin tonë, në disa raste mund t'ju duhet të përmbysni vlerën RateAxz për shkak të pozicionit fizik të xhiroskopit në lidhje me përshpejtuesin - kryeni përsëri testin e mësipërm, duke e rrotulluar pajisjen përreth boshti Y, këtë herë monitoroni daljen X të përshpejtuesit (AdcRx në modelin tonë). Nëse AdcRx rritet (90 shkallët e para të rrotullimit nga pozicioni horizontal), atëherë AdcGyroXZ gjithashtu duhet të rritet. Përndryshe ju duhet të përmbysni RateAxz, ju mund ta arrini këtë duke futur një faktor shenjë në Eq.3, si më poshtë:
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / Sensitivity, ku InvertAxz është 1 ose -1
e njëjta kallam testi bëhet për RateAyz, duke e rrotulluar pajisjen rreth boshtit X, dhe ju mund të identifikoni se cili prodhim xhiroskopi korrespondon me RateAyz, dhe nëse duhet të përmbyset. Pasi të keni vlerën për InvertAyz, duhet të përdorni formulën e mëposhtme për të llogaritur RateAyz:
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / Ndjeshmëria
Nëse i bëni këto teste në tabelën Acc_Gyro do të merrni rezultatet e mëposhtme:
- kunja dalëse për RateAxz është GX4 dhe InvertAxz = -1. - kunja dalëse për RateAyz është GY4 dhe InvertAyz = -1
Nga kjo pikë e tutje ne do të konsiderojmë që ju keni konfiguruar IMU -në tuaj në atë mënyrë që të mund të llogaritni vlerat e sakta për Axr, Ayr, Azr (siç përcaktohet në Pjesën 1. Përshpejtuesi) dhe RateAxz, RateAyz (siç përcaktohet në Pjesën 2. Xhiroskopi) Tjetra ne do të analizojmë marrëdhëniet midis këtyre vlerave që rezultojnë të dobishme për të marrë një vlerësim më të saktë të prirjes së pajisjes në lidhje me rrafshin e tokës.
Ju mund ta pyesni veten në këtë pikë, nëse modeli i akselerometrit na ka dhënë tashmë kënde prirjeje të Axr, Ayr, Azr pse do të donim të shqetësoheshim me të dhënat e xhiroskopit? Përgjigja është e thjeshtë: të dhënave të përshpejtuesit nuk mund t'i besohen gjithmonë 100%. Ka shumë arsye, mbani mend se përshpejtuesi mat forcën inerciale, një forcë e tillë mund të shkaktohet nga gravitacioni (dhe në mënyrë ideale vetëm nga graviteti), por gjithashtu mund të shkaktohet nga nxitimi (lëvizja) e pajisjes. Si rezultat edhe nëse akselerometri është në një gjendje relativisht të qëndrueshme, ai është akoma shumë i ndjeshëm ndaj dridhjeve dhe zhurmës mekanike në përgjithësi. Kjo është arsyeja kryesore pse shumica e sistemeve IMU përdorin një xhiroskop për të zbutur çdo gabim të përshpejtuesit. Por si bëhet kjo? Dhe a është xhiroskopi pa zhurmë?
Xhiroskopi nuk është i lirë nga zhurma megjithatë sepse mat rrotullimin është më pak i ndjeshëm ndaj lëvizjeve mekanike lineare, lloji i zhurmës nga i cili vuan përshpejtuesi, megjithatë xhiroskopët kanë lloje të tjera problemesh si p.sh. domethënia (nuk kthehet në vlerën e normës zero) kur rrotullimi ndalon). Sidoqoftë, duke mesatarizuar të dhënat që vijnë nga akselerometri dhe xhiroskopi, ne mund të marrim një vlerësim relativisht më të mirë të prirjes aktuale të pajisjes sesa do të merrnim duke përdorur vetëm të dhënat e përshpejtuesit.
Në hapat e ardhshëm do të prezantoj një algoritëm që është frymëzuar nga disa ide të përdorura në filtrin Kalman, megjithatë është shumë më i thjeshtë dhe më i lehtë për t'u zbatuar në pajisjet e ngulitura. Para kësaj, le të shohim së pari atë që duam të llogarisë algoritmi ynë. Epo, është drejtimi i vektorit të forcës së gravitetit R = [Rx, Ry, Rz] nga i cili mund të nxjerrim vlera të tjera si Axr, Ayr, Azr ose cosX, komod, cosZ që do të na japë një ide rreth prirjes së pajisjes sonë në lidhje me rrafshin tokësor, ne diskutojmë lidhjen midis këtyre vlerave në Pjesën 1. Dikush mund të thotë - a nuk i kemi tashmë këto vlera Rx, Ry, Rz nga Barazimi.2 në Pjesën 1? Epo po, por mbani mend se këto vlera rrjedhin vetëm nga të dhënat e përshpejtuesit, kështu që nëse do t'i përdorni ato drejtpërdrejt në aplikacionin tuaj, mund të merrni më shumë zhurmë sesa mund të tolerojë aplikacioni juaj. Për të shmangur konfuzionin e mëtejshëm, le të ri-përcaktojmë matjet e akselerometrit si më poshtë:
Racc - është vektori i forcës inerciale i matur me përshpejtues, që përbëhet nga komponentët e mëposhtëm (projeksionet në akset X, Y, Z):
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / Ndjeshmëria RyAcc = (AdcRy * Vref / 1023 - VzeroG) / Ndjeshmëria RzAcc = (AdcRz * Vref / 1023 - VzeroG) / Ndjeshmëria
Deri më tani ne kemi një grup vlerash të matura që mund t'i marrim thjesht nga vlerat ADC të përshpejtuesit. Ne do ta quajmë këtë grup të dhënash një "vektor" dhe ne do të përdorim shënimin e mëposhtëm.
Racc = [RxAcc, RyAcc, RzAcc]
Për shkak se këto përbërës të Racc mund të merren nga të dhënat e përshpejtuesit, ne mund ta konsiderojmë atë një hyrje në algoritmin tonë.
Ju lutemi vini re se për shkak se Racc mat forcën e gravitetit ju do të jeni të saktë nëse supozoni se gjatësia e këtij vektori të përcaktuar si më poshtë është e barabartë ose afër 1g.
| Racc | = SQRT (RxAcc^2 + RyAcc^2 + RzAcc^2), Sidoqoftë, për të qenë të sigurt, ka kuptim të azhurnoni këtë vektor si më poshtë:
Racc (normalizuar) = [RxAcc/| Racc |, RyAcc/| Racc |, RzAcc/| Racc |].
Kjo do të sigurojë që gjatësia e vektorit tuaj të normalizuar Racc është gjithmonë 1.
Tjetra ne do të prezantojmë një vektor të ri dhe do ta quajmë atë
Pushim = [RxEst, RyEst, RzEst]
Ky do të jetë rezultati i algoritmit tonë, këto janë vlera të korrigjuara bazuar në të dhënat e xhiroskopit dhe bazuar në të dhënat e vlerësuara të së kaluarës.
Këtu është ajo që do të bëjë algoritmi ynë: - përshpejtuesi na thotë: "Tani jeni në pozicionin Racc" - ne themi "Faleminderit, por më lejoni të kontrolloj", - pastaj korrigjoni këtë informacion me të dhënat e xhiroskopit, si dhe me të dhënat e pushimit të kaluar dhe nxjerrim një vektor të ri të vlerësuar Rest. - ne e konsiderojmë Pushimin si "bastin tonë më të mirë" për pozicionin aktual të pajisjes.
Le të shohim se si mund ta bëjmë atë të funksionojë.
Ne do të fillojmë sekuencën tonë duke besuar në akselerometrin tonë dhe duke caktuar:
Pushim (0) = Racc (0)
Nga rruga kujtoni Rest dhe Racc janë vektorë, kështu që ekuacioni i mësipërm është vetëm një mënyrë e thjeshtë për të shkruar 3 grupe ekuacionesh dhe për të shmangur përsëritjen:
RxEst (0) = RxAcc (0) RyEst (0) = RyAcc (0) RzEst (0) = RzAcc (0)
Tjetra ne do të bëjmë matje të rregullta në intervale të barabarta kohore prej T sekondash, dhe do të marrim matje të reja që do t'i përcaktojmë si Racc (1), Racc (2), Racc (3) etj. Ne gjithashtu do të nxjerrim vlerësime të reja në çdo intervale kohore Pushim (1), Pushim (2), Pushim (3) etj.
Supozoni se jemi në hapin n. Ne kemi dy grupe vlerash të njohura që duam të përdorim:
Pushimi (n -1) - vlerësimi ynë i mëparshëm, me Pushim (0) = Racc (0) Racc (n) - matja jonë aktuale e akselerometrit
Para se të llogarisim Pushimin (n), le të prezantojmë një vlerë të re të matur, që mund të marrim nga xhiroskopi ynë dhe një vlerësim i mëparshëm.
Ne do ta quajmë Rgyro, dhe është gjithashtu një vektor i përbërë nga 3 përbërës:
Rgyro = [RxGyro, RyGyro, RzGyro]
Ne do ta llogarisim këtë vektor një komponent në të njëjtën kohë. Do të fillojmë me RxGyro.
Le të fillojmë duke vëzhguar lidhjen e mëposhtme në modelin tonë të xhiroskopit, nga trekëndëshi me kënd të drejtë i formuar nga Rz dhe Rxz mund të nxjerrim atë:
tan (Axz) = Rx/Rz => Axz = atan2 (Rx, Rz)
Atan2 mund të jetë një funksion që nuk e keni përdorur më parë, është i ngjashëm me atan, përveçse kthen vlerat në rangun e (-PI, PI) në krahasim me (-PI/2, PI/2) siç kthehet nga atani, dhe merr 2 argumente në vend të një. Na lejon të konvertojmë dy vlerat e Rx, Rz në kënde në rangun e plotë prej 360 gradë (-PI në PI). Mund të lexoni më shumë rreth atan2 këtu.
Pra, duke ditur RxEst (n-1), dhe RzEst (n-1) mund të gjejmë:
Axz (n-1) = atan2 (RxEst (n-1), RzEst (n-1)).
Mos harroni se xhiroskopi mat shkallën e ndryshimit të këndit Axz. Pra, ne mund të vlerësojmë këndin e ri Axz (n) si më poshtë:
Axz (n) = Axz (n-1) + ShkallaAxz (n) * T
Mos harroni se RateAxz mund të merret nga leximet tona ADC të xhiroskopit. Një formulë më e saktë mund të përdorë një normë mesatare të rrotullimit të llogaritur si më poshtë:
RateAxzAvg = (RateAxz (n) + RateAxz (n-1)) / 2 Axz (n) = Axz (n-1) + RateAxzAvg * T
Në të njëjtën mënyrë mund të gjejmë:
Ayz (n) = Ayz (n-1) + ShkallaAyz (n) * T
Ok tani kemi Axz (n) dhe Ayz (n). Ku shkojmë nga këtu për të zbritur RxGyro/RyGyro? Nga barazimi 1 mund të shkruajmë gjatësinë e vektorit Rgyro si më poshtë:
| Rgyro | = SQRT (RxGyro^2 + RyGyro^2 + RzGyro^2)
Gjithashtu për shkak se ne normalizuam vektorin tonë Racc, mund të supozojmë se gjatësia e tij është 1 dhe nuk ka ndryshuar pas rrotullimit, kështu që është relativisht e sigurt të shkruhet:
| Rgyro | = 1
Le të miratojmë një shënim të shkurtër të përkohshëm për llogaritjet më poshtë:
x = RxGyro, y = RyGyro, z = RzGyro
Duke përdorur marrëdhëniet e mësipërme, ne mund të shkruajmë:
x = x / 1 = x / SQRT (x^2+y^2+z^2)
Le të ndajmë numëruesin dhe emëruesin e thyesës me SQRT (x^2 + z^2)
x = (x / SQRT (x^2 + z^2)) / SQRT ((x^2 + y^2 + z^2) / (x^2 + z^2))
Vini re se x / SQRT (x^2 + z^2) = sin (Axz), pra:
x = sin (Axz) / SQRT (1 + y^2 / (x^2 + z^2))
Tani shumëzoni numëruesin dhe emëruesin e thyesës brenda SQRT me z^2
x = mëkat (Axz) / SQRT (1 + y^2 * z^2 / (z^2 * (x^2 + z^2)))
Vini re se z / SQRT (x^2 + z^2) = cos (Axz) dhe y / z = tan (Ayz), kështu që më në fund:
x = sin (Axz) / SQRT (1 + cos (Axz)^2 * tan (Ayz)^2)
Duke u kthyer në shënimin tonë marrim:
RxGyro = mëkat (Axz (n)) / SQRT (1 + cos (Axz (n))^2 * tan (Ayz (n))^2)
në të njëjtën mënyrë e gjejmë atë
RyGyro = mëkat (Ayz (n)) / SQRT (1 + cos (Ayz (n))^2 * tan (Axz (n))^2)
Tani, më në fund mund të gjejmë:
RzGyro = Shenjë (RzGyro)*SQRT (1 - RxGyro^2 - RyGyro^2).
Ku Shenja (RzGyro) = 1 kur RzGyro> = 0, dhe Shenja (RzGyro) = -1 kur RzGyro <0.
Një mënyrë e thjeshtë për ta vlerësuar këtë është marrja:
Shenjë (RzGyro) = Shenjë (RzEst (n-1))
Në praktikë kini kujdes kur RzEst (n-1) është afër 0. Ju mund ta kaloni krejtësisht fazën xhiro në këtë rast dhe caktoni: Rgyro = Pushim (n-1). Rz përdoret si një referencë për llogaritjen e këndeve Axz dhe Ayz dhe kur është afër 0, vlerat mund të tejmbushin dhe të shkaktojnë rezultate të këqija. Do të jeni në domenin e numrave të mëdhenj të pikave lundruese ku zbatimet e funksionit tan () / atan () mund të kenë mungesë saktësie.
Pra, le të përmbledhim atë që kemi deri më tani, ne jemi në hapin n të algoritmit tonë dhe kemi llogaritur vlerat e mëposhtme:
Racc - leximet aktuale nga përshpejtuesi ynë Rgyro - marrë nga Pushimi (n -1) dhe leximet aktuale të xhiroskopit
Cilat vlera përdorim për të llogaritur vlerësimin e përditësuar Pushimi (n)? Me siguri keni menduar se ne do t'i përdorim të dyja. Ne do të përdorim një mesatare të ponderuar, në mënyrë që:
Pushim (n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
Ne mund ta thjeshtojmë këtë formulë duke pjesëtuar numëruesin dhe emëruesin e thyesës me w1.
Pushim (n) = (Racc * w1/w1 + Rgyro * w2/w1)/(w1/w1 + w2/w1)
dhe pas zëvendësimit të w2/w1 = wGyro marrim:
Pushimi (n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
Në forumin e mësipërm wGyro na tregon se sa i besojmë xhiros tonë në krahasim me përshpejtuesin tonë. Kjo vlerë mund të zgjidhet në mënyrë eksperimentale, zakonisht vlerat midis 5..20 do të shkaktojnë rezultate të mira.
Dallimi kryesor i këtij algoritmi nga filtri Kalman është se kjo peshë është relativisht e fiksuar, ndërsa në filtrin Kalman peshat azhurnohen përgjithmonë bazuar në zhurmën e matur të leximeve të përshpejtuesit. Filtri Kalman është përqendruar në dhënien e rezultateve teorike "më të mira", ndërsa ky algoritëm mund t'ju japë rezultate "mjaft të mira" për aplikimin tuaj praktik. Ju mund të zbatoni një algoritëm që rregullon wGyro në varësi të disa faktorëve të zhurmës që matni, por vlerat fikse do të funksionojnë mirë për shumicën e aplikacioneve.
Ne jemi një hap larg nga marrja e vlerave tona të përditësuara të vlerësuara:
RxEst (n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro) RyEst (n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro) RzEst (n) = (RzAcc + RzGyro * wGyro) / (1 + wGyro)
Tani le ta normalizojmë përsëri këtë vektor:
R = SQRT (RxEst (n)^2 + RyEst (n)^2 + RzEst (n)^2)
RxEst (n) = RxEst (n)/R RyEst (n) = RyEst (n)/R RzEst (n) = RzEst (n)/R
Dhe ne jemi gati të përsërisim lakun tonë përsëri.
Ky udhëzues u shfaq fillimisht në starlino.com, unë kam bërë disa redaktime të lehta dhe e kam postuar përsëri me leje. Faleminderit Starlino!
Recommended:
Platforma e kontrolluar me sensorë gyro për enigmën labirint: 3 hapa

Platforma e kontrolluar nga Gyro Sensor për Maze Puzzle: Ky udhëzues u krijua në përmbushje të kërkesës së projektit të kursit Make në Universitetin e Floridës së Jugut (www.makecourse.com) " Ky projekt i thjeshtë i frymëzuar nga një platformë vetë-balancuese që merr reagime nga akceleroma
Roll and Pitch Axis Gimbal për GoPro duke përdorur Arduino - Servo dhe MPU6050 Gyro: 4 hapa

Roll and Pitch Axis Gimbal për GoPro Duke përdorur Arduino - Servo dhe MPU6050 Gyro: Ky udhëzues u krijua në përmbushje të kërkesës së projektit të Makecourse në Universitetin e Floridës së Jugut (www.makecourse.com) Qëllimi i këtij projekti ishte të ndërtonte një Gimbal me 3 akse për GoPro duke përdorur Arduino nano + 3 servo motorë +
Një stacion tjetër moti Arduino (ESP-01 & BMP280 & DHT11 & OneWire): 4 hapa
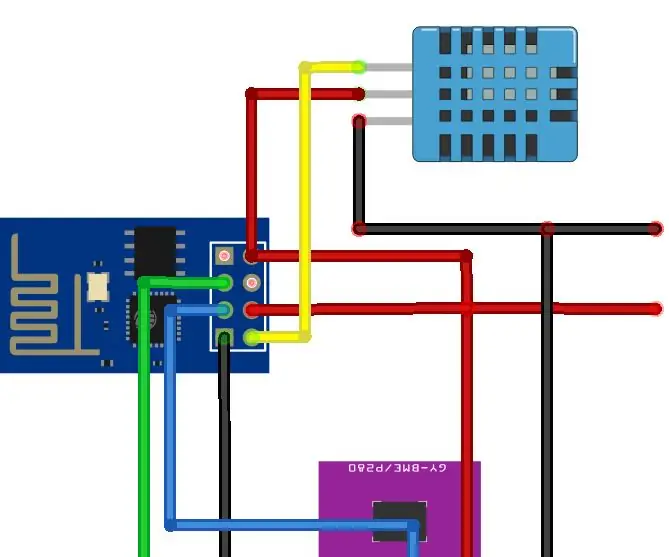
Edhe një Stacion Moti Arduino (ESP-01 & BMP280 & DHT11 & OneWire): Këtu mund të gjeni një përsëritje të përdorimit të OneWire me kunjat e pakta të një ESP-01. Pajisja e krijuar në këtë udhëzues lidhet me rrjetin Wifi të pajisjes tuaj zgjedhje (duhet të keni kredencialet …) Mbledh të dhëna shqisore nga një BMP280 dhe një DHT11
DIY MusiLED, LED të sinkronizuara me muzikë me aplikacionin Windows & Linux me një klik (32-bit & 64-bit). Lehtë për t’u rikrijuar, e lehtë për t’u përdorur, e lehtë për t’

DIY MusiLED, LED të sinkronizuara me muzikë me aplikacionin Windows & Linux me një klik (32-bit & 64-bit). Lehtë për t'u rikrijuar, e lehtë për t'u përdorur, e lehtë për t'u transferuar.: Ky projekt do t'ju ndihmojë të lidhni 18 LED (6 të kuqe + 6 blu + 6 të verdhë) në bordin tuaj Arduino dhe të analizoni sinjalet e Kartës së Zërit të kompjuterit tuaj në kohë reale dhe t'i transmetoni ato në LED për t'i ndezur ato sipas efekteve të rrahjes (Snare, High Hat, Kick)
Arduino Nano dhe Visuino: Shndërroni përshpejtimin në kënd nga përshpejtuesi dhe xhiroskopi Sensori MPU6050 I2C: 8 hapa (me fotografi)
Arduino Nano dhe Visuino: Shndërroni Përshpejtimin në Kënd Nga Përshpejtuesi dhe Xhiroskopi Sensori MPU6050 I2C: Pak kohë më parë kam postuar një tutorial se si mund të lidhni Përshpejtuesin, Xhiroskopin dhe Compass Sensorin me Arduino Nano dhe ta programoni me Visuino për të dërguar të dhëna dhe pako të ekranit atë në një fushëveprim dhe instrumente vizuale. Përshpejtuesi dërgon X, Y,
