Robot vetë -balancues duke përdorur algoritmin PID (STM MC): 9 hapa

2024 Autor: John Day | [email protected]. E modifikuara e fundit: 2024-01-30 12:27

Kohët e fundit është bërë shumë punë në vetë -balancimin e objekteve. Koncepti i vetë -balancimit filloi me balancimin e lavjerrësit të përmbysur. Ky koncept u shtri në dizajnin e avionëve gjithashtu. Në këtë projekt, ne kemi hartuar një model të vogël të robotit vetë -balancues duke përdorur algoritmin PID (proporcional, integral, derivativ). Që atëherë, kjo metodë është fytyra e re e sistemeve të kontrollit të procesit industrial. Ky raport rishikon metodat e përfshira në vetë -balancimin e objekteve. Ky projekt u realizua si një projekt semestral për të kuptuar korrelacionin e PID me efikasitetin e proceseve të ndryshme industriale. Këtu ne fokusohemi vetëm në ofrimin e një rishikimi të shkurtër mbi efikasitetin dhe zbatimin e kontrollit të PID. Ky punim është zhvilluar duke ofruar një hyrje të shkurtër në sistemet e kontrollit dhe terminologjitë përkatëse, me shtimin e motivimeve për projektin. Janë bërë eksperimente dhe vëzhgime, meritat dhe dobësitë e përshkruara me përfundimin në përmirësimet e ardhshme. Një model i robotit vetë -balancues u zhvillua për të kuptuar efikasitetin e PID në botën e sistemit të kontrollit. Duke kaluar nëpër disa teste dhe eksperimente rigoroze, meritat dhe dobësitë e sistemit të kontrollit PID u zbuluan. U zbulua se përkundër shumë përparësive të kontrollit PID mbi metodat e kaluara, prapëseprapë ky sistem kërkon shumë përmirësime. Shpresohet që lexuesi të ketë një kuptim të mirë të rëndësisë së vetë -balancimit, efikasitetit dhe mangësive të kontrollit të PID

Hapi 1: Hyrje

Me ardhjen e kompjuterëve dhe industrializimin e proceseve, gjatë historisë njerëzore, ka pasur gjithmonë kërkime për të zhvilluar mënyra për të rindërtuar proceset dhe më e rëndësishmja, për t'i kontrolluar ato duke përdorur makina në mënyrë autonome. Qëllimi është të zvogëlojë përfshirjen e njeriut në këto procese, duke zvogëluar kështu gabimin në këto procese. Prandaj, u zhvillua fusha e "Inxhinierisë së Sistemit të Kontrollit". Inxhinieria e Sistemit të Kontrollit mund të përcaktohet si përdorimi i metodave të ndryshme për të kontrolluar funksionimin e një procesi ose mirëmbajtjen e një mjedisi konstant dhe të preferuar, qoftë manual apo automatik.

Një shembull i thjeshtë mund të jetë kontrolli i temperaturës në një dhomë. Kontrolli manual nënkupton praninë e një personi në një vend që kontrollon kushtet aktuale (sensorin), e krahason atë me vlerën e dëshiruar (përpunimi) dhe ndërmerr veprimet e duhura për të marrë vlerën e dëshiruar (aktivizuesin). Problemi me këtë metodë është se nuk është shumë i besueshëm pasi një person është i prirur ndaj gabimit ose neglizhencës në punën e tij. Gjithashtu, një problem tjetër është se shkalla e procesit të nisur nga aktivizuesi nuk është gjithmonë e njëtrajtshme, që do të thotë se ndonjëherë mund të ndodhë më shpejt sesa kërkohet ose ndonjëherë mund të jetë e ngadaltë. Zgjidhja e këtij problemi ishte përdorimi i një mikrokontrolluesi për të kontrolluar sistemin. Mikrokontrolluesi është

programuar për të kontrolluar procesin, sipas specifikimeve të dhëna, të lidhura në një qark (për t'u diskutuar më vonë), ushqyer vlerën ose kushtet e dëshiruara dhe në këtë mënyrë kontrollon procesin për të ruajtur vlerën e dëshiruar. Avantazhi i këtij procesi është se nuk kërkohet ndërhyrje njerëzore në këtë proces. Gjithashtu, shkalla e procesit është uniforme

Sistemi bazë i kontrollit

Diagrami i mëparshëm tregon një version shumë të thjeshtuar të një Sistemi Kontrolli. Mikrokontrolluesi është në zemër të çdo Sistemi Kontrolli. Isshtë një komponent shumë i rëndësishëm prandaj, zgjedhja e tij e përzgjedhjes duhet të bëhet me kujdes bazuar në kërkesat e Sistemit. Mikrokontrolluesi merr një hyrje nga përdoruesi. Ky hyrje përcakton gjendjen e dëshiruar të Sistemit. Mikrokontrolluesi gjithashtu merr një informacion kthyes nga sensori. Ky sensor është i lidhur me daljen e Sistemit, informacioni i të cilit kthehet në hyrje. Mikroprocesori, bazuar në programimin e tij, kryen llogaritjet e ndryshme dhe i jep një dalje aktivizuesit. Aktivizuesi, bazuar në prodhimin, kontrollon uzinën që të përpiqet të ruajë ato kushte. Një shembull mund të jetë një drejtues motori që drejton një motor ku drejtuesi i motorit është aktivizuesi dhe motori është impianti. Motori, kështu rrotullohet me një shpejtësi të caktuar. Sensori i lidhur lexon gjendjen e uzinës në kohën e tanishme dhe e furnizon atë me mikrokontrolluesin. Mikrokontrolluesi përsëri krahason, bën llogaritjet dhe kështu, cikli përsëritet. Ky proces është i përsëritur dhe i pafund, ku mikrokontrolluesi ruan kushtet e dëshiruara

Hapi 2: Sistemi i kontrollit i bazuar në PID

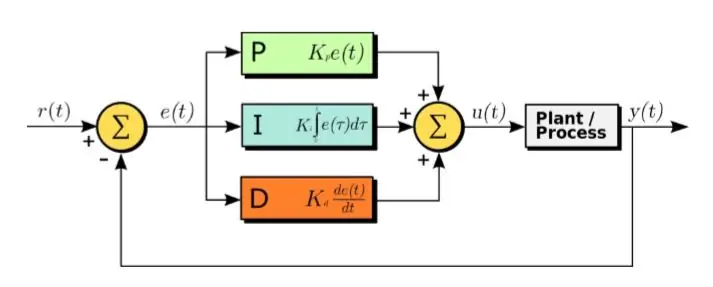
Algoritmi PID është një metodë efikase e dizajnimit të një sistemi kontrolli.

Përkufizimi

PID qëndron për Proportional, Integral dhe Derivativ. Në këtë algoritëm, sinjali i gabimit i marrë është hyrja. Dhe ekuacioni i mëposhtëm zbatohet në sinjalin e gabimit

U (t) = Kp ∗ e (t) + Kd ∗ d/dt (e (t)) + Ki ∗ integrale (e (t)) (1.1)

Shpjegim i shkurtër

Siç mund të shihet në ekuacionin e mësipërm, integrali dhe derivati i sinjaleve të gabimit llogariten, shumëzohen me konstantet e tyre përkatëse dhe shtohen së bashku me konstanten Kp të shumëzuar me e (t). Dalja më pas i jepet aktivizuesit i cili e bën sistemin të funksionojë. Tani le të shikojmë secilën pjesë të funksionit me radhë. Ky funksion ndikon drejtpërdrejt në kohën e ngritjes, kohën e rënies, kulmin mbi goditjen, kohën e zgjidhjes dhe gabimin e gjendjes së qëndrueshme.

• Pjesa proporcionale: Pjesa proporcionale zvogëlon kohën e ngritjes dhe zvogëlon gabimin e gjendjes së qëndrueshme. Kjo do të thotë që sistemit do t’i duhet më pak kohë për të arritur vlerën e tij kulmore dhe kur të arrijë gjendjen e tij të qëndrueshme, gabimi i gjendjes së qëndrueshme do të jetë i ulët. Sidoqoftë, ajo rrit tejkalimin e pikut.

• Pjesa derivative: Pjesa derivative zvogëlon tejkalimin dhe kohën e zgjidhjes. Kjo do të thotë që gjendja kalimtare e sistemit do të jetë më e lagur. Gjithashtu, sistemi do të arrijë gjendjen e tij të qëndrueshme në një kohë më të vogël. Sidoqoftë, nuk ka ndonjë efekt në kohën e rritjes ose gabimin e gjendjes së qëndrueshme.

• Pjesa integrale: Pjesa integrale zvogëlon kohën e ngritjes dhe eliminon plotësisht gabimin e gjendjes së qëndrueshme. Sidoqoftë, ajo rrit tejkalimin e pikut dhe kohën e zgjidhjes.

• Akordimi: Një sistem i mirë kontrolli do të ketë kohë të ulët ngritjeje, kohë zgjidhjeje, kulm të tejkalimit dhe gabim të gjendjes së qëndrueshme. Prandaj, Kp, Kd, Ki duhet të rregullohen saktësisht për të rregulluar kontributin e faktorëve të mësipërm në mënyrë që të fitohet një Sistem i mirë Kontrolli.

Figura është bashkangjitur duke treguar efektin e ndryshimit të parametrave të ndryshëm në algoritmin PID.

Hapi 3: Roboti vetë -balancues

Një robot vetë-balancues është një robot me shumë shtresa, me dy rrota.

Roboti do të përpiqet të balancojë veten në aplikimin e çdo force (ve) të pabarabartë. Ai do të ekuilibrojë veten me aplikimin e forcës që kundërshton rezultatin e forcave në robot.

Metodat e vetë -balancimit

Ekzistojnë katër metoda të vetë -balancimit të robotëve. Këto janë si më poshtë:

Vetë -balancimi duke përdorur sensorin e pjerrësisë me dy IR

Kjo është një nga mënyrat më të vrazhda për të balancuar robotin pasi kërkon shumë më pak harduer dhe një algoritëm relativisht të lehtë. Në këtë qasje, dy sensorë IR të pjerrët përdoren për të matur distancën midis tokës dhe robotit. Bazuar në distancën e llogaritur, PID mund të përdoret për të drejtuar motorët për të balancuar robotin në përputhje me rrethanat. Një disavantazh i kësaj metode është se sensori IR mund të humbasë disa lexime. Një problem tjetër është se një ndërprerje dhe sythe kërkohen për llogaritjen e distancës e cila rrit kompleksitetin kohor të algoritmit. Prandaj, kjo metodë e balancimit të robotit nuk është shumë efikase.

Vetë -Balancimi duke përdorur Accelerometer

Përshpejtuesi na jep nxitimin e trupit në 3 akse. Përshpejtimi i orientuar në boshtin y (lart) dhe boshtin x (përpara) na jep masën për të llogaritur drejtimin e gravitetit dhe kështu llogaritur këndin e pjerrësisë. Këndi llogaritet si më poshtë:

θ = arctan (Ay/Ax) (1.2)

Disavantazhi i përdorimit të kësaj metode është se gjatë lëvizjes së robotit, nxitimi horizontal gjithashtu do të shtohet në leximet që është një zhurmë me frekuencë të lartë. Prandaj, këndi i prirjes do të jetë i pasaktë.

Vetë -Balancimi duke përdorur Xhiroskop

Një xhiroskop përdoret për të llogaritur shpejtësitë e këndit përgjatë tre boshteve. Këndi i pjerrësisë merret duke përdorur ekuacionin e mëposhtëm.

θp (i) = θp (i − 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1.3)

Një disavantazh i madh i përdorimit të xhiroskopit është se ai ka një paragjykim të vogël DC i cili është një zhurmë me frekuencë të ulët dhe në pak kohë vlerat e kthyera janë krejtësisht të gabuara. Kjo, pas integrimit, do të bëjë që pika zero të largohet. Si rezultat i tij, roboti do të qëndrojë në pozicionin e tij vertikal për ca kohë dhe do të bjerë përmbys pasi të vijë zhvendosja.

Vetë -Balancimi duke përdorur si Accelerometer ashtu edhe Xhiroskop

Siç u diskutua më lart, përdorimi i vetëm një akselerometri ose xhiroskopi nuk do të na japë këndin e duhur të pjerrësisë. Për të shpjeguar këtë, përdoren akselerometri dhe xhiroskopi. Këto të dyja janë të ngulitura në MPU6050. Në këtë ne marrim të dhënat nga të dy ata dhe pastaj i bashkojmë ato ose duke përdorur Kalman Filter ose Filter Plotësues.

• Filtri Kalman: Filteri Kalman llogarit vlerësimin më të mirë të gjendjes së një sistemi dinamik nga matjet e zhurmshme, duke minimizuar gabimin mesatar në katror të vlerësimit. Ai funksionon në dy faza, parashikimi dhe korrigjimi, duke pasur parasysh ekuacionet diskrete stokastike që përshkruajnë dinamikën e sistemit. Sidoqoftë, është një algoritëm shumë kompleks për t'u zbatuar veçanërisht në një pajisje të kufizuar të një mikrokontrolluesi.

• Filtri Plotësues: Ky algoritëm përdor kryesisht të dhënat e marra nga xhiroskopi dhe i integron ato me kalimin e kohës për të marrë këndin e pjerrësisë. Përdor gjithashtu një pjesë të vogël të leximeve të përshpejtuesit. Filtri plotësues, në fakt, minimizon zhurmën me frekuencë të lartë të përshpejtuesit dhe zhurmën me frekuencë të ulët të xhiroskopit dhe pastaj i bashkon ato për të dhënë këndin më të mirë të prirjes.

Hapi 4: Dizajni i Robotit

Ne kemi krijuar një robot vetë -balancues duke përdorur kontrolluesin Proportional Derivativ të zbatuar nga Filter Plotësues për MPU6050. Ky model i vogël i Robotit vetë -balancues do të na ilustrojë dobinë e sistemeve të kontrollit në vetë -balancimin e robotëve.

Zbatimi i sistemit:

Sistemi është një robot vetë -balancues. Shtë zbatuar duke përdorur PID Controller i cili është një Kontrollues Proportional Integral Derivativ. Ne e balancojmë robotin duke drejtuar rrotat e tij në drejtim të rënies së tij. Duke vepruar kështu, ne po përpiqemi të mbajmë qendrën e gravitetit të robotit mbi pikën e boshtit. Për të drejtuar rrotat në drejtim të rënies së tij, duhet të dimë se ku bie roboti dhe shpejtësinë me të cilën po bie. Këto të dhëna merren duke përdorur MPU6050 e cila ka një akselerometër dhe një xhiroskop. MPU6050 mat këndin e pjerrësisë dhe i jep prodhimin e tij Mikrokontrolluesit. MPU6050 është i ndërlidhur me Bordin STM përmes I2C. Në I2C, një tel është për orën e cila quhet SCL. Një tjetër është për transferimin e të dhënave që është SDA. Në këtë, përdoret komunikimi i skllevërve master. Adresa fillestare dhe adresa përfundimtare është e specifikuar për të ditur se nga fillojnë të dhënat dhe ku mbarojnë. Ne kemi zbatuar Filtrin Plotësues këtu për MPU6050 i cili është një filtër matematikor për të bashkuar rezultatet e përshpejtuesit dhe xhiroskopit. Pas marrjes së të dhënave nga MPU6050, mikrokontrolluesi do të bëjë llogaritjet për të ditur se ku po bie. Bazuar në llogaritjet, mikrokontrolluesi STM do t'i japë komandat shoferit të motorit që të drejtojë automjetet në drejtim të rënies, gjë që do të balancojë robotin.

Hapi 5: Komponentët e projektit

Komponentët e mëposhtëm u përdorën në projektin e robotit vetë -balancues:

STM32F407

Një mikrokontrollues i projektuar nga ST Microelectronics. Punon në Arkitekturën ARM Cortex-M.

Shofer Motor L298N

Ky IC përdoret për të drejtuar motorin. Ai merr dy hyrje të jashtme. Një nga mikrokontrolluesi i cili i jep atij një sinjal PWM. Duke rregulluar gjerësinë e pulsit, shpejtësia e motorit mund të rregullohet. Hyrja e tij e dytë është burimi i tensionit i kërkuar për të drejtuar motorin i cili është një bateri 12V në rastin tonë.

Motor DC

Një motor DC funksionon me një furnizim DC. Në këtë eksperiment, DC Motor po punon duke përdorur çiftëzuesit optikë të lidhur me drejtuesin e motorit. Për të drejtuar motorin ne kemi përdorur Motor Drive L298N.

MPU6050

MPU6050 përdoret për të marrë informacionin se ku bie roboti. Ai mat këndin e pjerrësisë në lidhje me pikën zero të pjerrësisë e cila është pozicioni i MPU6050 kur programi fillon të funksionojë.

MPU6050 ka një akselerometër me 3 boshte dhe një xhiroskop me 3 boshte. Përshpejtuesi mat përshpejtimin përgjatë tre akseve dhe xhiroskopi mat shpejtësinë këndore për të tre akset. Për të kombinuar daljen, ne duhet të filtrojmë zhurmat e të dyjave. Për të filtruar zhurmat, ne kemi Kalman dhe filtër plotësues. Ne kemi zbatuar filtër plotësues në projektin tonë.

Çifti Opto 4N35

Optokoupler është një pajisje e përdorur për të izoluar pjesën e tensionit të ulët dhe atë të tensionit të lartë të qarkut. Siç sugjeron edhe emri, funksionon në bazë të dritës. Kur pjesa e tensionit të ulët merr një sinjal, rryma rrjedh në pjesën e tensionit të lartë

Hapi 6: Struktura e Robotit

Struktura e robotit shpjegohet si më poshtë:

Struktura Fizike

Roboti vetë-balancues përbëhet nga dy shtresa të përbëra nga qelqi plastik transparent. Detajet e dy shtresave janë dhënë më poshtë:

Shtresa e parë

Në pjesën e poshtme të shtresës së parë, ne kemi vendosur një qelizë për të fuqizuar bordin STM. Gjithashtu dy motorë prej 4 volt secili janë vendosur në secilën anë me goma të lidhura që roboti të lëvizë. Në pjesën e sipërme të shtresës së parë, dy bateri prej 4 volt secila (gjithsej 8 volt) dhe drejtuesi i motorit IC (L298N) janë vendosur për funksionimin e motorëve.

Shtresa e dytë

Në shtresën e sipërme të robotit, ne kemi vendosur Bordin STM në Perf Board. Një tabelë tjetër perf me 4 bashkues opto është vendosur në shtresën e sipërme. Xhiroskopi vendoset gjithashtu në shtresën e sipërme të robotit nga ana e poshtme. Të dy përbërësit janë vendosur në pjesën e mesme në mënyrë që qendra e gravitetit të mbahet sa më e ulët.

Qendra e Gravitetit të Robotit

Qendra e gravitetit mbahet sa më e ulët. Për këtë qëllim, ne kemi vendosur bateri të rënda në shtresën e poshtme dhe komponentë të lehtë të tillë si bordi STM dhe optocouplers në shtresën e sipërme.

Hapi 7: Kodi

Kodi u përpilua në Atollic TrueStudio. Studio STM u përdor për qëllime korrigjimi.

Hapi 8: Përfundimi

Pas shumë eksperimenteve dhe vëzhgimeve, ne përfundimisht arrijmë në pikën ku përmbledhim rezultatet tona dhe diskutojmë se deri ku kemi arritur në zbatimin dhe përpunimin e efikasitetit të sistemit.

Rishikimi i Përgjithshëm

Gjatë eksperimentimit, shpejtësia e motorit u kontrollua me sukses duke përdorur algoritmin PID. Kurba megjithatë nuk është saktësisht një vijë e drejtë e lëmuar. Ka shumë arsye për këtë:

• Sensori edhe pse i lidhur me një filtër të ulët kalimi akoma siguron debouncings të caktuara të caktuara; këto janë për shkak të rezistencave jo lineare dhe disa arsye të pashmangshme të elektronikës analoge.

• Motori nuk rrotullohet pa probleme nën tension të vogël ose PWM. Ai siguron lëvizje që mund të shkaktojnë disa vlera të gabuara të ushqyera në sistem.

• Për shkak të lëkundjes, sensori mund të humbasë disa çarje që ofrojnë vlera më të larta. • Një arsye tjetër kryesore për gabimet mund të jetë frekuenca e orës bazë të mikrokontrolluesit STM. Ky model i mikrokontrolluesit STM siguron një orë bazë prej 168MHz. Megjithëse u trajtua me këtë problem në këtë projekt, ekziston një nocion i përgjithshëm në lidhje me këtë model që nuk siguron saktësisht një frekuencë kaq të lartë.

Shpejtësia e lakut të hapur siguron një vijë shumë të qetë me vetëm disa vlera të papritura. Algoritmi PID po punon gjithashtu duke siguruar një kohë shumë të ulët të vendosjes së motorit. Algoritmi PID i motorit u testua nën tensione të ndryshme duke mbajtur konstante shpejtësinë e referencës. Ndryshimi i tensionit nuk ndryshon shpejtësinë e motorit duke treguar se Algoritmi PID po punon përfundimisht

Efektiviteti

Këtu ne diskutojmë efikasitetin e kontrolluesit PID që kemi vërejtur gjatë eksperimentimit.

Zbatimi i Thjeshtë

Ne kemi parë në seksionin e eksperimenteve dhe vëzhgimeve se një kontrollues PID është shumë i lehtë për t'u zbatuar. Kërkon vetëm tre parametra ose konstante që duhet të vendosen në mënyrë që të ketë një sistem të kontrollit të shpejtësisë

Efikasitet i pakrahasueshëm për sistemet lineare

Kontrolluesi PID linear është më efikas në familjen e kontrolluesve sepse logjika është shumë e thjeshtë dhe aplikimi është i përhapur në rast të aplikimeve lineare ose mjaft lineare.

Kufizimet

Ne shpjeguam në mënyrë abstrakte për Kufizimet e këtij sistemi. Këtu ne diskutojmë disa prej tyre që kemi vëzhguar.

Përzgjedhja e Konstanteve

Ne kemi parë që, megjithëse një kontrollues PID është i lehtë për t'u zbatuar, prapëseprapë është një pengesë e madhe e sistemit që hapi i përzgjedhjes së vlerës së konstantave është i mundimshëm; pasi dikush duhet të bëjë llogaritjet e vështira. Mënyra tjetër është metoda e goditjes dhe provës, por kjo gjithashtu nuk është efikase.

Konstantet jo gjithmonë konstante

Rezultatet eksperimentale treguan se për vlera të ndryshme të shpejtësisë referuese për motorin, kontrolluesi PID nuk funksionoi për të njëjtat vlera të konstanteve PID. Për shpejtësi të ndryshme, konstantet duheshin zgjedhur në mënyrë të ndryshme dhe kjo rrit koston llogaritëse në mënyrë eksponenciale.

Jo lineare

Kontrolluesi PID i përdorur në rastin tonë është linear, prandaj, mund të aplikohet vetëm në sistemet lineare. Për sistemet jo-lineare, kontrolluesi duhet të zbatohet në mënyrë të ndryshme. Megjithëse ekzistojnë metoda të ndryshme jo lineare të PID, ato kërkojnë më shumë parametra për t'u zgjedhur. Kjo përsëri e bën sistemin të padëshirueshëm për shkak të kostos së lartë llogaritëse.

Kërkohet shtytje fillestare

Ne treguam në pjesën e eksperimentimit se për një shpejtësi relativisht të vogël referimi ku gabimi është mjaft i vogël në fillim, PWM i furnizuar nga PID është aq i vogël sa nuk gjeneron çift rrotulluesin e kërkuar fillestar për motorin. Pra, motori në disa prova nuk funksionon ose në prova të tjera siguron një tejkalim të madh dhe një kohë më të gjatë zgjidhjeje.

Hapi 9: Faleminderit special

Faleminderit të veçantë për anëtarët e grupit tim që më ndihmuan gjatë këtij projekti.

Së shpejti do të ngarkoj lidhjen e videos.

Shpresoj se do ta gjeni interesant këtë udhëzues.

Ky është Tahir Ul Haq nga nënshkrimi i UET. Urime !!!