A dini për rregullimin ESP32 ADC ?: 29 hapa

2024 Autor: John Day | [email protected]. E modifikuara e fundit: 2024-01-30 12:20

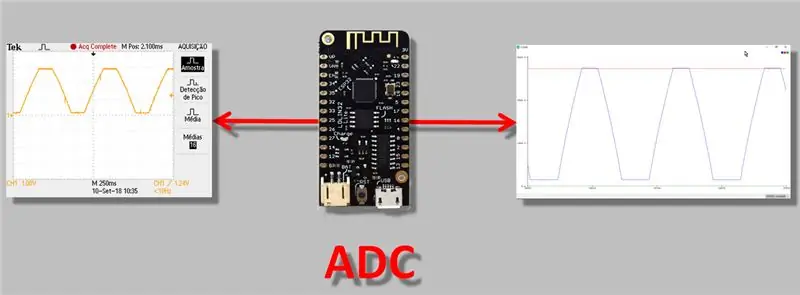
Sot, unë do të flas për një çështje më teknike, por një që unë mendoj se të gjithë ata që punojnë me ESP32 duhet ta dinë: çështja e ADC (konvertuesi analog në dixhital) lexon rregullimin. Më duket e rëndësishme sepse kur bëni një "matje", veçanërisht me një instrument që ka një dalje analoge, duhet të jeni absolutisht të sigurt se leximi po kryhet në mënyrë korrekte.

Prandaj, në videon sot, ne do të kryejmë matje duke përdorur "konvertuesin analog-dixhital" të ESP32, do të vëzhgojmë mospërputhjet e konvertimit dhe do të aplikojmë një metodë përshtatjeje / kalibrimi ADC.

Hapi 1: Çfarë është një AD Converter?

Një konvertues AD është një qark i aftë për të përkthyer një sasi analoge (të vazhdueshme) në vlera dixhitale (diskrete). Cfare do te thote ajo? Do të thotë që ndërsa vlerat dixhitale mund të marrin vetëm vlera diskrete të formuara nga kombinimi i zerove dhe atyre, një sasi analoge mund të marrë çdo vlerë brenda një diapazoni. Për shembull, nëse matim tensionin e një qelize ideale AA, mund të gjejmë çdo vlerë midis 0V dhe 1.5V, pasi kjo është sasi analoge. Gjendja e daljes së një llambë ideale duhet të marrë vetëm dy gjendje (fikur ose ndezur), që është një madhësi diskrete. Meqenëse mikrokontrolluesit punojnë duke përdorur këtë logjikë diskrete, ne kemi nevojë për një qark të aftë për të përkthyer një sasi analoge në dixhitale (ose diskrete).

Hapi 2: Burimet e përdorura

• Një kartë Lolin32 Lite v1.0.0

• Një oshiloskop Tektronix TDS1001C për kapje

• Një kabllo USB për ESP32

• Një oshiloskop Hantek DSO4102C si gjenerator sinjali

Hapi 3: ESP32 ADC

Sipas të dhënave të Espressif, patate të skuqura ESP32 mund të paraqesin një ndryshim +/- 6% nga një çip në tjetrin në rezultatet e matura.

Për më tepër, konvertimi NUK ka një përgjigje lineare për çdo gamë të disponueshme për lexim. Espressif siguron një metodë për kalibrimin dhe sugjeron që përdoruesit të zbatojnë metoda të tjera nëse e konsiderojnë të nevojshme për të arritur saktësinë e dëshiruar.

Ne do të kryejmë një marrje të të dhënave, dhe nga kjo, ne do të tregojmë përgjigjet e ADC dhe një shembull të aplikimit të një procesi matematikor për të lexuar rregullimin.

Ka disa mënyra (më të thjeshta ose më komplekse) për të arritur këto rregullime. Varet nga ju që të vlerësoni më të përshtatshmet për projektin tuaj.

Ajo që tregohet këtu do të ketë një qëllim ilustrues dhe do të përpiqet të trajtojë pika interesante që mund të vërehen gjatë rregullimeve.

Hapi 4: Qarku i përdorur

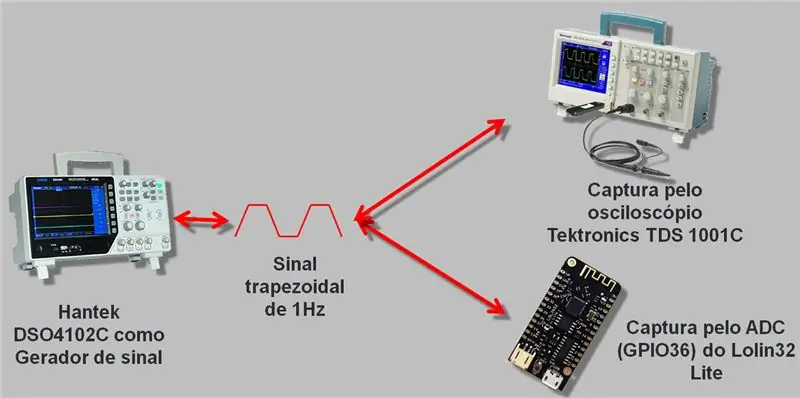
Kam përdorur një oshiloskop me një gjenerator sinjali që shkon deri në 25 MHz, Hantek DSO4102C. Ne krijuam një valë që u lexua nga ESP A / D dhe oshiloskopi. Të dhënat e mbledhura u regjistruan në csv dhe në një tabelë, të cilën do ta lë në fund të artikullit për shkarkim.

Hapi 5: Shenja e përdorur

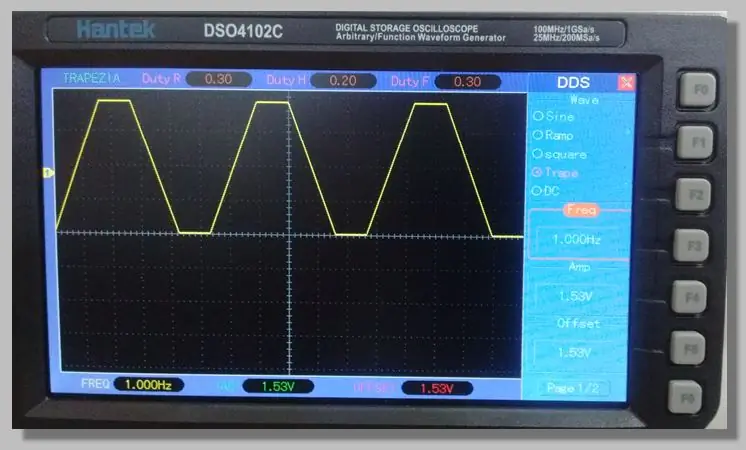
Ne zgjodhëm një sinjal trapezoid me frekuencë të ulët i cili lejon hyrjen në rampat që kalojnë në të gjithë gamën e konvertimit. Kjo lejon një numër të madh mostrash në këto rampa.

Hapi 6: Të dhënat e marra nga osciloskopi

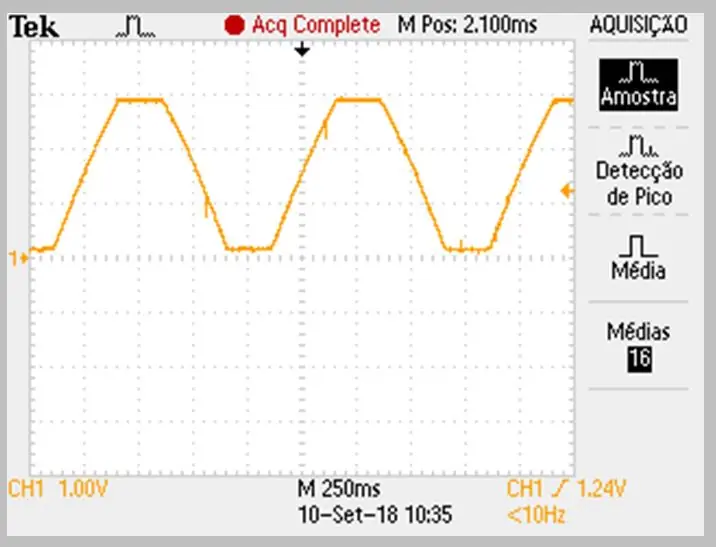
Imazhi i kapjes u krye nga një oshiloskop. Të dhënat u ruajtën në një skedar csv. Vini re lakimin e lehtë në rampat në rritje dhe rënie të sinjalit.

Hapi 7: Të dhënat e marra nga osciloskopi (skedari csv në Excel)

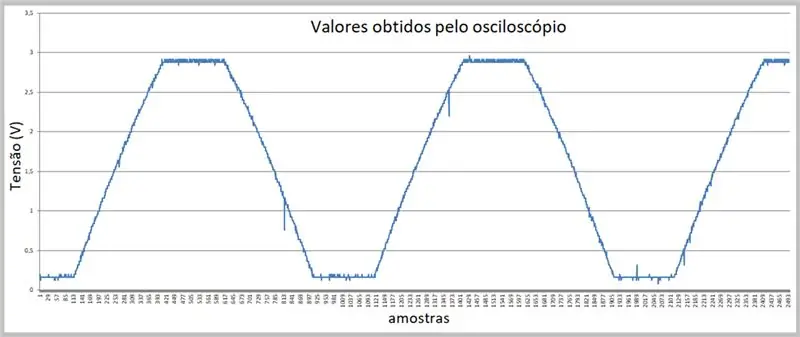
Ne kemi mostrat këtu.

Hapi 8: Të dhënat e marra nga ADC

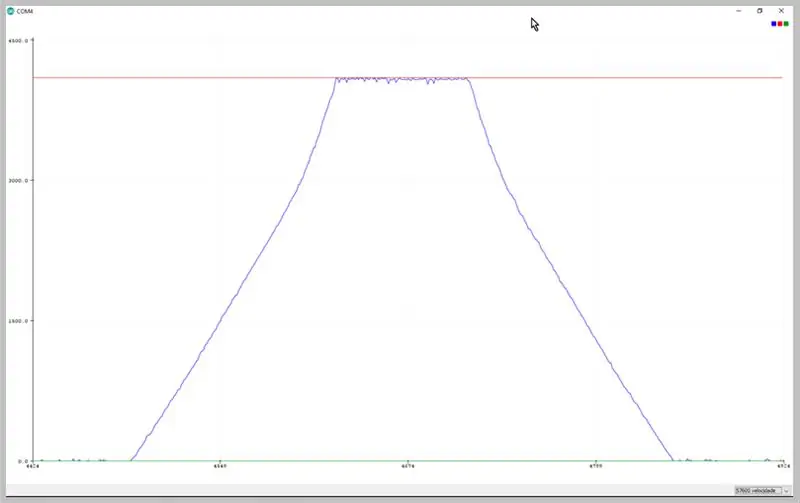
Duke ndryshuar shkallën e transferimit të serisë, ne mund të shikojmë të dhënat e kapura nga ADC. Vëzhgoni deformimin e sinjalit trapezoidal.

Të dhënat e vëzhguara në komplotuesin serik të Arduino IDE

Hapi 9: Të dhënat e marra nga ADC - Excel

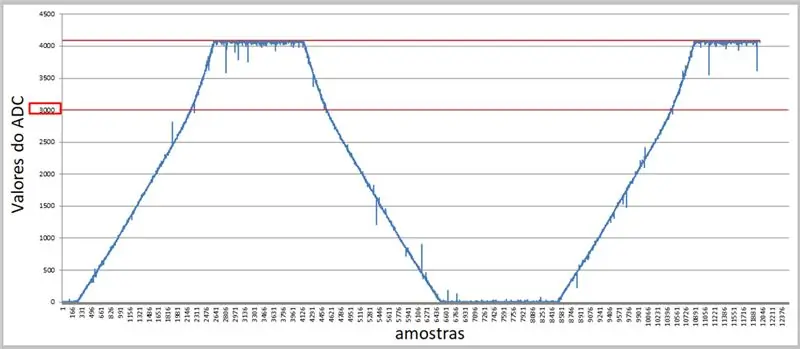
Duke përdorur një normë më të lartë dhe terminalin serik, ne mund të kapim vlerat dhe t'i zbatojmë ato në Excel për krahasimet tona.

Hapi 10: Krahasimi i Rampave të Ngjitjes

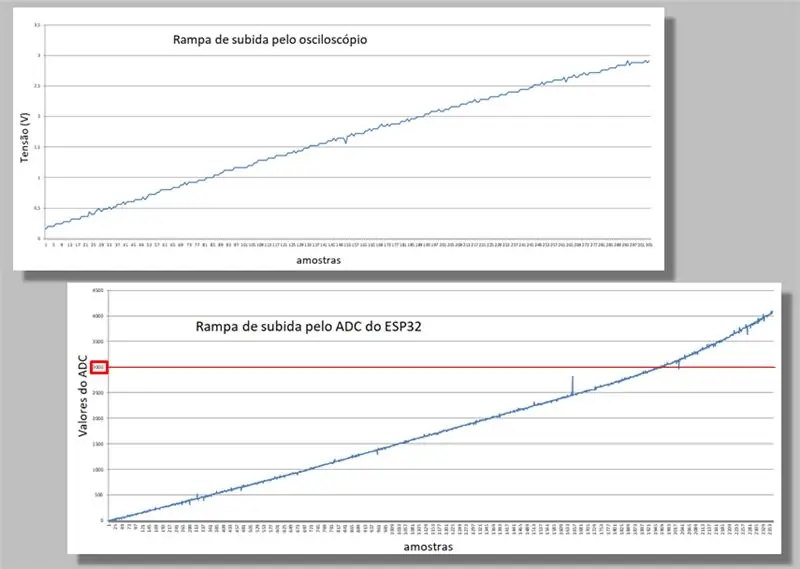
Ne krahasojmë dy rampat ngjitëse të dy kapjeve.

Vini re lakimin që ndodh në të dy rampat.

Vini re gjithashtu se për të njëjtën devijim, ne kemi shumë më tepër mostra të ESP32 sesa nga oshiloskopi.

Hapi 11: Barazimi i numrit të mostrave

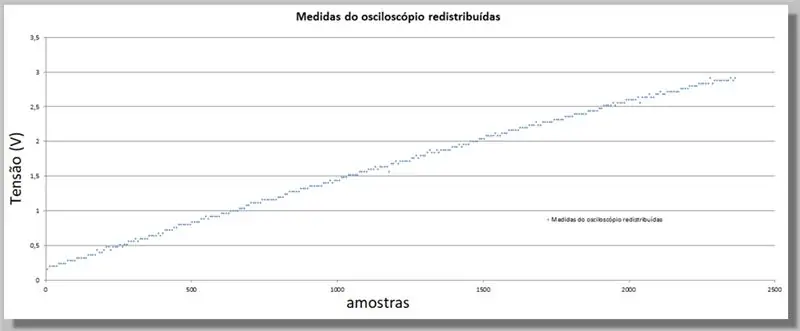
Për shkak se ESP32 siguroi një numër më të madh mostrash sesa oshiloskopi, ne duhet të barazojmë këto vlera, pasi ato do të shërbejnë si një indeks për të krahasuar dy kthesat.

Për këtë, ne do të bëjmë një krahasim të drejtpërdrejtë.

Ne kemi 305 mostra për devijimin e oshiloskopit dhe 2365 mostra për devijimin ADC.

Meqenëse rampat janë të së njëjtës gamë, mund të themi se kemi afërsisht 7.75 mostra të ADC për secilin oshiloskop.

Shumëzimi i indeksit të secilit mostër të oshiloskopit ka të njëjtën kurbë, por me indekse ekuivalente me ADC dhe të dhënat e rishpërndara.

Për të plotësuar të dhënat që mungojnë për pozicionet e reja, ne do të aplikojmë një kurbë që i përshtatet statistikisht të dhënave të njohura.

Hapi 12: Plotësimi i Boshllëqeve - Linja e Trendit

Duke përzgjedhur të dhënat e njohura (pikat blu), duke klikuar dhe më pas duke klikuar me butonin e djathtë, ne zgjedhim: "Shto linjën e trendit …"

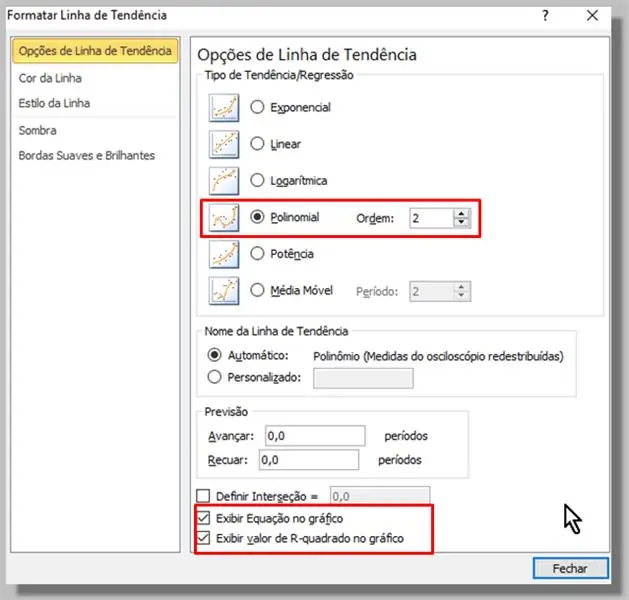
Në dritaren që shfaqet, ne zgjedhim llojin Polinomial (rendi 2 do të jetë i mjaftueshëm).

Ne gjithashtu kontrolluam opsionet "Shihni ekuacionin në tabelë" dhe "Shfaqni vlerën e katrorit R në tabelë".

Ne klikojmë "Mbyll".

Hapi 13: Plotësimi i Boshllëqeve - Kurba Polinomale e Klasës 2

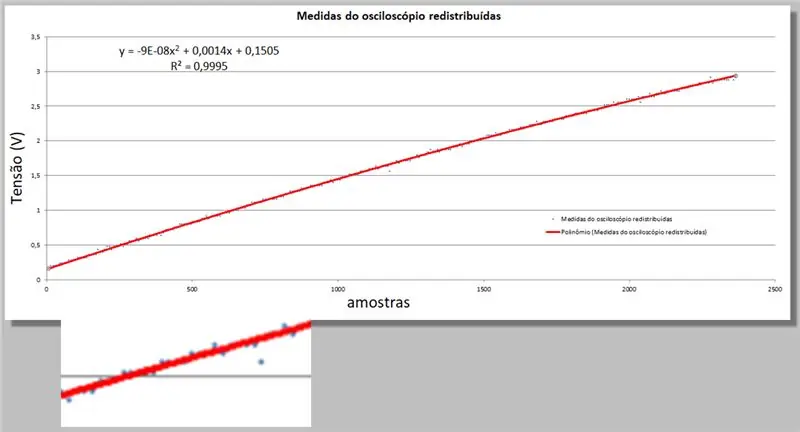
Excel na jep dy pjesë të reja informacioni; ekuacioni i rendit të dytë që i përshtatet më së miri të dhënave, dhe ekuacioni i katrorit R që përcakton këtë mjaftueshmëri.

Vetëm mos harroni se sa më afër 1, aq më i përshtatshëm është ekuacioni.

Le të mos thellohemi në matematikën e përfshirë, le ta përdorim vetëm si mjet.

Hapi 14: Plotësimi i boshllëqeve - Vlerësimi i funksionit

Le të plotësojmë boshllëqet e kampionimit me të dhënat e krijuara nga ekuacioni. Dhe pastaj, krahasojini ato pikë për pikë.

y = -9E -08x2 + 0, 0014x + 0, 1505

R² = 0, 9999

Tensioni i osciloskopit = -9E -08 * indeksi 2 + 0, 0014 * indeksi + 0, 1505

Hapi 15: Shndërrimi i Tensionit të Osciloskopit në një Vlerë Ekuivalente për t'u Krahasuar me ADC

Le të përfitojmë nga kjo për të transformuar vlerën e tensionit të oshiloskopit në një vlerë ekuivalente ADC.

Meqenëse vlera më e lartë e marrë në ADP të ESP32 ishte 4095, e cila është ekuivalente me leximin e 2.958V për të njëjtin indeks, mund të themi se:

Çdo volt në matjet e oshiloskopit është i barabartë me afërsisht 1384.4 njësi të Krishtit. Prandaj, ne mund të shumëzojmë të gjitha matjet e oshiloskopit me këtë vlerë.

Hapi 16: Krahasimi i dy Rampave të Marra

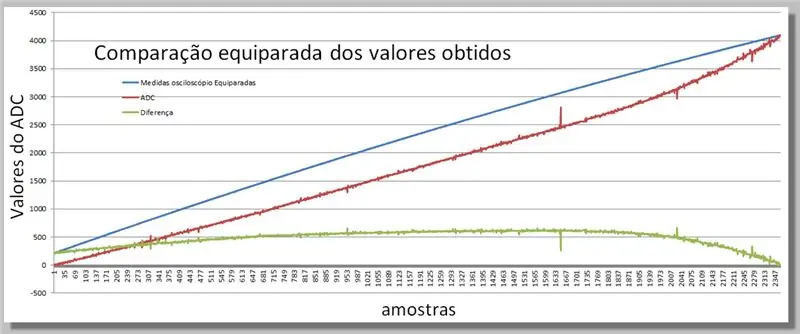
Vizualizimi i dallimeve të marra në dy leximet.

Hapi 17: Sjellja e Diferencës së Leximit ADC (ERROR)

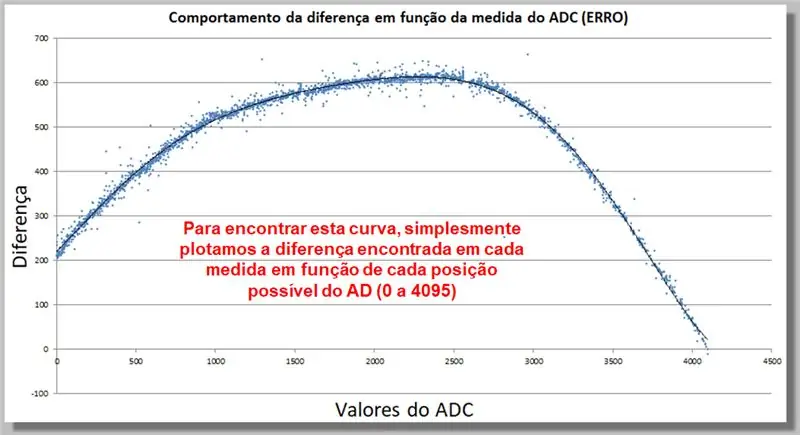
Kurba më poshtë tregon se si sillet ndryshimi në leximin ADC si një funksion i matjes. Ky koleksion i të dhënave do të na lejojë të gjejmë një funksion korrigjimi.

Për të gjetur këtë kurbë, ne thjesht vizatojmë diferencën e gjetur në secilën masë si funksion të çdo pozicioni të mundshëm të Krishtit (0 në 4095).

Hapi 18: Sjellja e ndryshimit të leximit ADC - Gjetja e një funksioni korrigjues

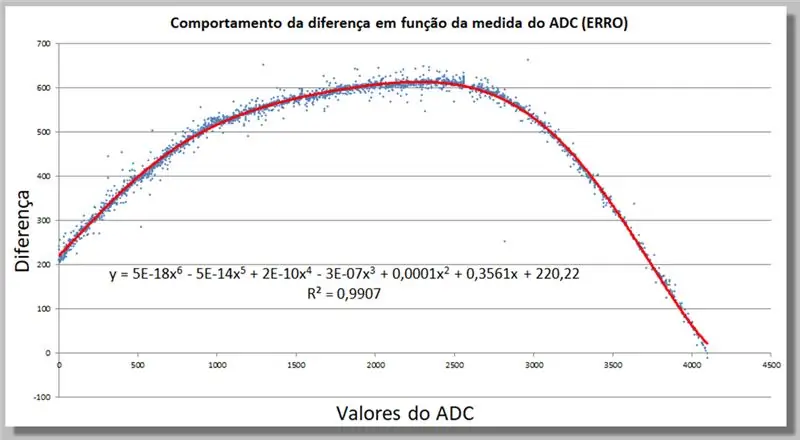
Ne mund të përcaktojmë në Excel një funksion korrigjimi duke shtuar një Trend Line, tani të një shkalle më të lartë, derisa të përshtatet mjaftueshëm me të dhënat tona.

Hapi 19: Përdorimi i programeve të tjera

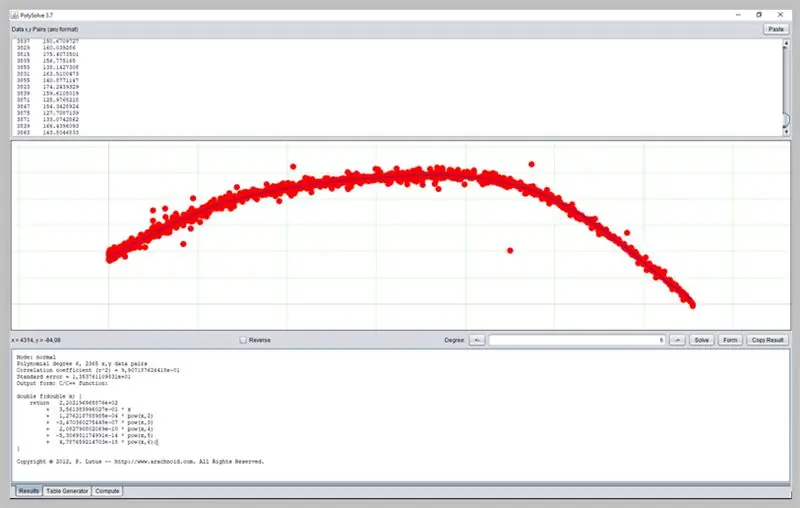
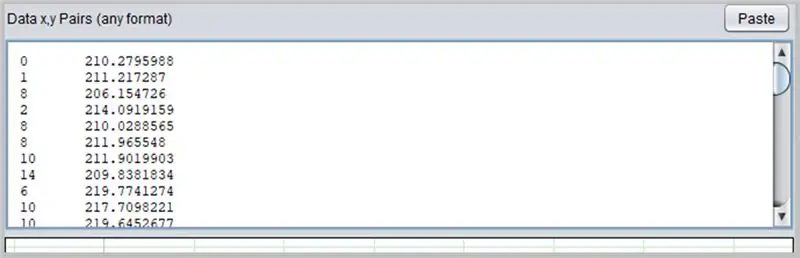
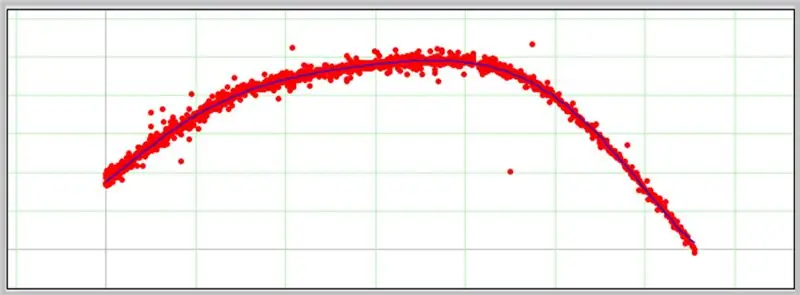
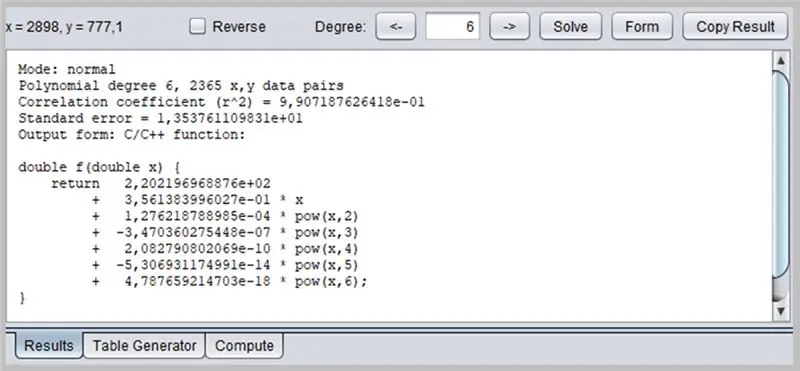
Softuer tjetër interesant për përcaktimin e kthesave është PolySolve, i cili mund të përdoret drejtpërdrejt në lidhjen: https://arachnoid.com/polysolve/ ose të shkarkohet si një aplikacion Java.

Lejon aplikimin e regresioneve polinomikë të shkallës më të lartë dhe dhënien e funksionit të formatuar, si dhe funksionalitete të tjera.

Për t'i përdorur ato, thjesht futni të dhënat në kutinë e parë të tekstit. Të dhënat duhet të ndjekin rendin X, Y të ndarë me presje ose skedë. Bëni kujdes në përdorimin e saktë të pikës si pikë dhjetore.

Një tabelë do të shfaqet në kutinë tjetër nëse të dhënat e futura janë formatuar saktë.

Ja se si shkoi kurba jonë e gabimit ADC.

Kjo dritare do të paraqesë rezultatin e regresionit, duke përfshirë të dhënat e mjaftueshmërisë së funksionit, të cilat nga ana e tyre mund të kenë formatimin e prodhimit në disa mënyra: si një funksion C / C ++, një listë koeficientësh, një funksion i shkruar në Java, etj.

Shënim: Kushtojini vëmendje ndarësve dhjetorë

Hapi 20: Konstantet dhe konfigurimi ()

Unë theksoj këtu GPIO e përdorur për kapjen analoge. Filloj portën serike, si dhe kunjin e përcaktuar për kapjen analoge.

const int pin_leitura = 36; // GPIO përdor për kapjen e analogica void setup () {Serial.begin (1000000); // Filloni një somente portale për debug pinMode (pin_leitura, INPUT); // Pino utilizado para captura analógica}

Hapi 21: Loop () dhe Funksioni Korrigjues

Ne bëjmë kapjen e tensionit të rregulluar dhe i printojmë vlerat me ose pa korrigjimet e sakta.

lak void () {int valor_analogico = analogRead (pin_leitura); // realiza a captura da tensão ajustada //Serial.print(valor_analogico + f (valor_analogico)); // imprime os valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimime os valores para debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Serial.println (0); // cria uma linha para marcar o valor mínimo de 0}

Vini re në rreshtin 12 që kemi mundësinë e printimit të të dhënave me shtimin e funksionit të diferencës f (analog_value).

Hapi 22: Përdorimi i funksionit të korrigjimit PolySolve

Këtu, ne përdorim funksionin PolySolve brenda Arduino IDE.

/* Mënyra: Shkalla normale Polinomiale 6, 2365 x, çifte të të dhënave Koeficienti i korrelacionit (r^2) = 9, 907187626418e-01 Gabim standard = 1, 353761109831e+01 Forma e daljes: Funksioni C/C ++: E drejta e autorit © 2012, P. Lutus - https://www.arachnoid.com. Të gjitha të drejtat e rezervuara. */ double f (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Vini re ndryshimin e presjes për pikë si ndarës dhjetor.

Hapi 23: Regjistrohuni me Korrigjim - Serial Plotter

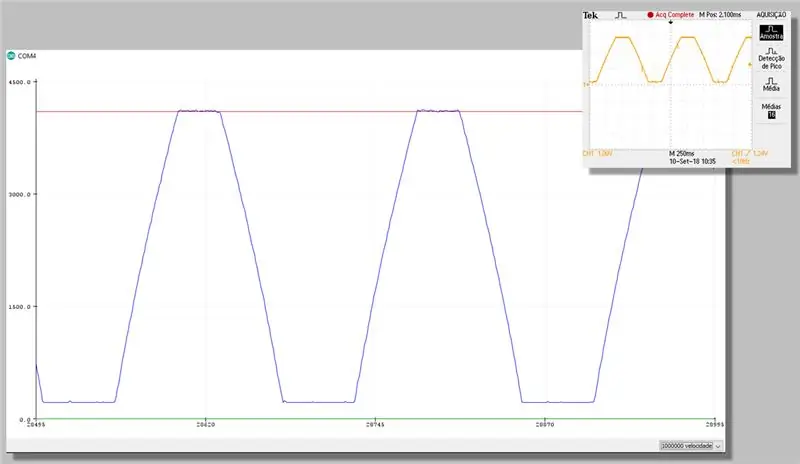
Hapi 24: Kostoja Llogaritëse

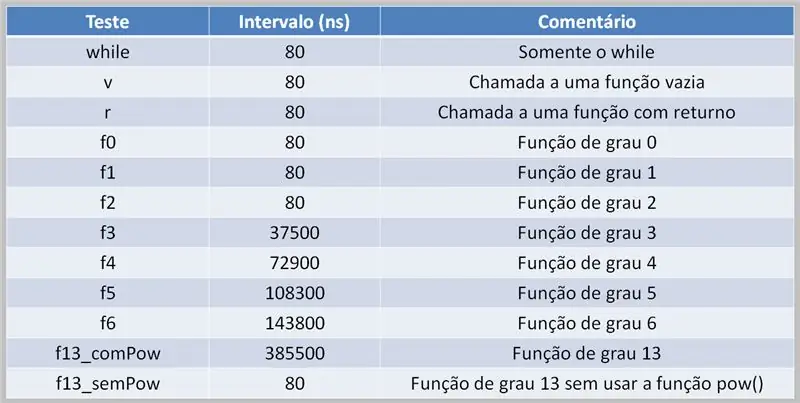
Për të kryer llogaritjet polinomiale, është e nevojshme që procesori të merret me këtë detyrë. Kjo mund të çojë në vonesa në ekzekutim, në varësi të kodit burimor dhe fuqisë llogaritëse në dispozicion.

Këtu, ne shohim një tabelë rezultati të një testi duke përdorur polinome shumë shkallë. Vini re ndryshimin midis kohëve kur funksioni pow () ishte përdorur dhe kur nuk ishte.

Hapi 25: Kodi i Testit - Konfigurimi () dhe fillimi i lakut ()

Këtu, ne kemi kodin e përdorur në testin tonë.

void setup () {Serial.begin (1000000); // Iniciando a porta serial somente para debug} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000.0; // quantidade de chamadas float contador = 0.0; // contador de chamadas

Hapi 26: Kodi i Testit - Loop () dhe Përpunimi

Kam përdorur funksionin micros () për të marrë vlerën në mikrosekonda.

// ============= inicia o processo float agora = micros (); // marca o instante inicial while (contador <quantidade) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a POW PUN // f13_comPow (valor_analogico); // grau 13º COM a função POW contador ++; } agora = (mikros () - agora) / kuantidade; // përcaktimi i një intervali që do të kalojë për herë të parë // ============== përfundimi i procesit

Hapi 27: Kodi i Testit - Lak () - Rezultatet

Ne shtypim vlerën e kthyer nga funksioni i klasës 13 me dhe pa POW për krahasim, si dhe intervalin e përpunimit.

// imprim o valide retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a Função POW Serial.print (" -"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM a Função POW Serial.print (" -"); // imprim o intervalo do processamento Serial.println (agora, 6); }

Hapi 28: Kodi i Testit - Funksionet e Përdorura

Funksionet boshe (vetëm me kthim) të shkallës 0 dhe 1.

// FUNÇÃO VAZIAdouble v (double x) {} // FUNÇÃO SOMENTE COM RETORNO double r (double x) {return x; } // FUNÇÃO DE GRAU 0 dyshe f0 (dyshe x) {kthimi 2.202196968876e+02; } // FUNÇÃO DE GRAU 1 dyshe f1 (dyshe x) {kthimi 2.202196968876e + 02 + 3.561383996027e-01 * x; }

Funksionet e klasës 2, 3 dhe 4.

// FUNÇÃO DE GRAU 2dyshe f2 (dyshe x) {kthimi 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 double f3 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3); } // FUNÇÃO DE GRAU 4 double f4 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * fuqi (x, 4); }

Funksionet e klasës 5 dhe 6.

// FUNÇÃO DE GRAU 5dyshe f5 (dyshe x) {kthimi 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * fuqi (x, 4) + -5.306931174991e-14 * fuqi (x, 5); } // FUNÇÃO DE GRAU 6 double f6 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Funksioni i klasës 13 duke përdorur POW.

// FUNÇÃO DE GRAU 13 USANDO O POWdouble f13_comPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }

Funksioni i klasës 13 pa përdorur POW.

// FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * * * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e -35 * x * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x * x; }

Hapi 29: Skedarët

Shkarkoni skedarët:

PDF

INO

Fletëllogaritëse