Zgjidhja e tabelave të së vërtetës: 10 hapa

2024 Autor: John Day | [email protected]. E modifikuara e fundit: 2024-01-30 12:11

Një tabelë e së vërtetës është një mënyrë për të vizualizuar të gjitha rezultatet e një problemi. Ky grup udhëzimesh është bërë për njerëzit që fillojnë në matematikë diskrete. Ne do të praktikojmë sot me një problem shembull që është specifik për këto udhëzime. Ju do të keni nevojë për një letër gërvishtëse dhe një laps për të vizualizuar tryezën. Ky problem duhet të zgjasë rreth 5 minuta për t'u kompletuar për njerëzit me njohuri paraprake në lidhje me temën dhe rreth 10 minuta për fillestarët.

Për këtë grup udhëzimesh, ne do të përqendrohemi në problemin ~ p Λ q. Ne po e përdorim këtë për të prezantuar disa simbole të nevojshme për të interpretuar tabelat e së vërtetës.

Hapi 1: Kuptimi i Tabelave të së Vërtetës

Një tabelë e së vërtetës është një mënyrë për të vizualizuar të gjitha mundësitë e një problemi. Njohja e tabelave të së vërtetës është një domosdoshmëri themelore për matematikën diskrete. Këtu, do të gjejmë të gjitha rezultatet për ekuacionin e thjeshtë të ~ p Λ q.

Hapi 2: Njohja e Simboleve

Hapi i parë në tabelën e së vërtetës është të kuptuarit e shenjave. "~" Në këtë problem të veçantë qëndron për mohim. "P" dhe "q" janë të dy ndryshore. "Λ" është ekuivalente me "dhe". Ky ekuacion lexohet si "jo p dhe q", domethënë, ekuacioni është i vërtetë nëse p nuk është i vërtetë dhe q është i vërtetë.

Hapi 3: Formatimi i tabelës

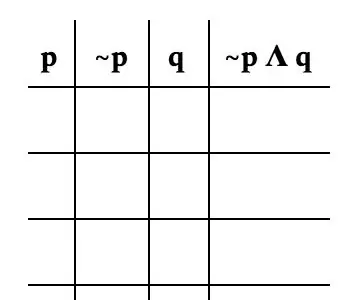
Tani për të formuar tabelën aktuale. Isshtë e rëndësishme që problemi të ndahet nga secila variabël. Për këtë problem, ne do ta ndajmë atë si më poshtë: p, ~ p, q dhe ~ p Λ q. Imazhi është një shembull i mirë se si duhet të duket tabela juaj.

Hapi 4: Caktimi i së vërtetës dhe të gabuarës

Meqenëse ekzistojnë vetëm dy ndryshore, do të ketë vetëm katër mundësi për ndryshore. Për p, ne e ndajmë atë me gjysmën e hapësirave të marra nga T (për të vërtetën) dhe gjysmën tjetër me F (për të rreme).

Hapi 5: Mohimi

Për ~ p, ju shkruani shenjën e kundërt që p ka pasi që ~ p është e kundërta e p.

Hapi 6: Variabli "q"

Për q, ju alternoni midis T dhe F në mënyrë që të merrni secilin kombinim të mundshëm. Meqenëse ekuacioni përqendrohet vetëm në ~ p, ne mund të injorojmë kolonën p kur përcaktojmë të vërtetën e ekuacionit. Simboli "Λ" do të thotë që të dyja ~ p dhe q duhet të jenë të vërteta që ekuacioni të jetë i vërtetë.

Hapi 7: Zgjidhja për të pavërtetën në kolonën e fundit

Për rreshtin e parë, meqë ~ p është F dhe q është T, ~ p Λ q është F në skenarin që ~ p është F dhe q është T. Skenari i vetëm ekuacioni është T është ku ~ p është T dhe q është T.

Hapi 8: Gjetja e së Vërtetës në Kolonën e Fundit

Kjo do të thotë se rreshti i vetëm që është T është i treti.

Hapi 9: Përfundimi i Tabelës

Kontrolloni dy herë që tabela juaj është e saktë. Ju e bëni këtë duke kontrolluar që shenjat tuaja janë të sakta dhe duke u siguruar që kolona e fundit është bërë në mënyrë korrekte. Kolona e fundit është rezultat i të gjitha ndryshimeve të mundshme nga ndryshoret.

Hapi 10: U krye

Tani që dini të bëni një tabelë themelore të së vërtetës, vazhdoni të praktikoni! Sa më shumë që praktikoni, aq më mirë do t’i bëni ato.